Виды бесконечностей: Виды бесконечностей и вынос мозга / Хабр
Бесконечность — это… Что такое Бесконечность?
Бесконечность — концепция, используемая в математике, философии и естественных науках. Бесконечность какого-то понятия или атрибута некоторого объекта означает невозможность указать для него границы или количественную меру. Точное значение этого термина несколько различается в зависимости от области применения — математика, физика, философия, теология или повседневная жизнь.
Потенциальная и актуальная бесконечность
Когда говорят, что некоторая величина потенциально бесконечна, то имеется в виду, что она может быть неограниченно увеличена. Альтернативой является понятие актуальной бесконечности, которая означает, что рассматривается (как реально существующая) величина, не имеющая конечной меры. Пример: второй постулат Евклида утверждает не бесконечность длины прямой линии, а всего лишь то, что «прямую можно непрерывно продолжать». Это потенциальная бесконечность. Если же рассмотреть всю бесконечную прямую, то она даёт пример актуальной бесконечности.
Античные философы и математики признавали, как правило, только потенциальную бесконечность, решительно отвергая возможность оперировать с актуально бесконечными атрибутами[1]. Соответственно этой доктрине формулировались научные утверждения. Например, теорема о бесконечности множества простых чисел у античных математиков формулировалась так: «Каково бы ни было простое число P, существует простое число, большее, чем P».
Аристотель писал:
… Всегда возможно придумать большее число, потому что количество частей, на которые можно разделить отрезок, не имеет предела. Поэтому бесконечность потенциальна, никогда не действительна; какое бы число делений ни задали, всегда потенциально можно поделить на большее число[2].
Именно Аристотель сделал большой вклад в осознание бесконечности, разделив её на потенциальную и актуальную и вплотную подойдя с этой стороны к основам математического анализа, а также указав на пять источников представления о ней:
- время;
- разделение величин;
- неиссякаемость творящей природы;
- само понятие границы, толкающее за её пределы;
- мышление, которое неостановимо.
Бесконечность в большинстве культур появилась как абстрактное количественное обозначение чего-то непостижимо большого, в применении к сущностям без пространственных или временных границ.
Математическому происхождению символа бесконечности предшествовал[3] религиозный аспект. Подобные символы были найдены среди Тибетских наскальных гравюр; змея, кусающая свой хвост, или змея бесконечности, часто изображается в форме такого символа.
Понятие бесконечности получило развитие в философии и теологии наравне с точными науками. К примеру, в теологии бесконечность Бога не столько даёт количественное определение, сколько означает неограниченность и непостижимость. В философии бесконечность долгое время рассматривалась также как атрибут пространства и времени; в наши дни это дискуссионный вопрос космологии. Например, древнейшим, первым известным, встречающимся в совершенно различных культурах символом бесконечности является змей Уроборос, иногда разворачиваемый в виде перевёрнутой восьмёрки.
В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы.[источник не указан 106 дней] К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие (биекцию), а целые числа включены в действительные. Таким образом, в этом случае «число элементов» (мощность) одного множества «бесконечней» «числа элементов» (мощности) другого. Основоположником этих понятий был немецкий математик Георг Кантор.
В математическом анализе ко множеству действительных чисел добавляются два символа и , применяющиеся для определения граничных значений и сходимости. Сто́ит отметить, что в этом случае речь об «осязаемой» бесконечности не идёт, так как любое утверждение, содержащее этот символ, можно записать, используя только конечные числа и кванторы. Эти символы, как и многие другие, были введены для сокращения записи более длинных выражений.
Символ
В 1655 году Джон Валлис издаёт большой трактат «О конических сечениях» (De sectionibus conicis), где на стр. 5 появляется придуманный им[4][5] символ бесконечности: ∞. В Юникоде бесконечность обозначена символом ∞ (U+221E), он включён в типографскую раскладку Бирмана версии 2.0 ( AltGr + 8 ).
См. также
Примечания
- ↑ Аристотель о бесконечности
- ↑ Физика III, 6.
- ↑ Robertson, Robin; Combs, Allan. The Uroboros // Indra’s Net: Alchemy and Chaos Theory as Models for Transformation. — Quest Books, 2009. — ISBN 9780835608626
- ↑ Scott, Joseph Frederick (1981), «The mathematical work of John Wallis, D.D., F.R.S., (1616-1703)» (2 ed.), AMS Bookstore, с. 24, ISBN 0-828-40314-7, <http://books.google.com/books?id=XX9PKytw8g8C> , Chapter 1, page 24
- ↑ «COLOG-88: International Conference on Computer Logic Tallinn, USSR, December 12–16, 1988: proceedings», Springer, 1990, с. 147, ISBN 3-540-52335-9, <http://books.google.com/books?id=nfnGohZvXDQC> , page 147
Литература
Ссылки
Бесконечность в математике. «Математическое бесконечное заимствовано из действительности, хотя и бессознательным образом, и поэтому оно может быть объяснено только из действительности, а не из самого себя, не из математической абстракции» (Энгельс Ф., Анти-Дюринг, 1966, с. 396). Материальная основа математического бесконечного может быть понята только при условии, что оно рассматривается в диалектическом единстве с конечным. Каждая математическая теория связана обязательным для неё требованием внутренней формальной непротиворечивости. Поэтому возникает вопрос о том, как соединить это требование с существенно противоречивым характером действительности: Б. «Уничтожение этого противоречия было бы концом бесконечности» (там же, с. 47). Ответ на этот вопрос заключается в следующем. Когда в теории пределов рассматриваются бесконечные пределы lim an = ¥, или в теории множеств ‒ бесконечные мощности, то это не приводит к внутренним формальным противоречиям в указанных теориях лишь потому, что эти различные специальные виды математических Б. являются лишь крайне упрощёнными, схематизированными образами различных сторон Б. действительного мира.
Задачи настоящей статьи ограничиваются указанием на различные подходы к Б. в математике, освещаемые подробнее в других статьях.
1) Представление о бесконечно малых и бесконечно больших переменных величинах является одним из основных в математическом анализе. Предшествовавшая современному подходу к понятию бесконечно малой концепция, по которой конечные величины составлялись из бесконечно большого числа бесконечно малых «неделимых» (см. «Неделимых» метод), трактовавшихся не как переменные, а как постоянные и меньшие любой конечной величины, может служить одним из примеров незаконного отрыва бесконечного от конечного: реальный смысл имеет только разложение конечных величин на неограниченно возрастающее число неограниченно убывающих слагаемых.
2) Совсем в другой логической обстановке Б.
появляется в математике в виде «несобственных» бесконечно удалённых геометрических образов (см. Бесконечно удалённые элементы). Здесь, например, бесконечно удалённая точка на прямой а рассматривается как особый постоянный объект, «присоединённый» к обычным конечным точкам. Однако неразрывная связь бесконечного с конечным обнаруживается и здесь, хотя бы при проектировании из центра, лежащего вне прямой, при котором бесконечно удалённой точке оказывается соответствующей прямая, проходящая через центр проектирования и параллельная основной прямой а.
Аналогичный характер имеет пополнение системы действительных чисел двумя «несобственными» числами +¥ и -¥, соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел 1, 2, 3,…, трансфинитными числами w, w + 1,…, 2w, 2w + 1,…. В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и «несобственными» бесконечно большими числами, рассматриваемыми как постоянные, ‒ с другой, возникли термины «потенциальная» Б. (для первых) и «актуальная» Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками актуальной и потенциальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла (как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математического анализа, должны восприниматься как «потенциальные». Наряду с этим в надлежащей логической обстановке в математику вполне закономерно входят и «актуальные» бесконечно большие «несобственные» числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы + ¥ и -¥ системы действительных чисел и т.д.).
В математике приходится иметь дело с двумя способами присоединения к числовой системе бесконечных «несобственных» элементов.
а) С проективной точки зрения на прямой находится одна «бесконечно удалённая точка». В обычной метрической системе координат этой точке естественно приписать абсциссу ¥. Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций
где Р (х) и Q (x) ‒ многочлены, в тех точках, где Q (x) имеет нуль более высокого порядка, чем Р (х), естественно положить f (x) = ¥. Для несобственного элемента ¥ устанавливаются такие правила действий:
¥ + а = ¥, если а конечно;
¥ + ¥ не имеет смысла;
¥ · а = ¥, если а ¹ 0;
¥ · 0 не имеет смысла.
Неравенства с участием ¥ не рассматриваются: бессмысленно спрашивать, больше или меньше ¥, чем конечное а.
б) При изучении действительных функций действительного переменного систему действительных чисел дополняют двумя несобственными элементами +¥ и -¥. Тогда можно положить, что -¥ < а < +¥ для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для +¥ и -¥ устанавливаются такие правила действий:
(+¥) + а = +¥, если а ¹ -¥;
(-¥) + а = -¥, если а ¹ +¥;
(+¥) + (-¥) лишено смысла;
(+¥) `·а = +¥, если а > 0;
(+¥) ` а = -¥, если а < 0;
(-¥) `·а = -¥, если a > 0;
(-¥) ` а = +¥, если а < 0;
(+¥) ` 0 и (¥) ` 0 лишены смысла.
В каждом математическом рассуждении следует отдавать себе отчёт, пользуемся мы в нём настоящей (не расширенной) числовой системой или расширенной, и в каком именно из двух указанных смыслов.
3) Основной интерес, но и основные трудности математического учения о Б. сосредоточиваются сейчас на вопросе о природе бесконечных множеств математических объектов. Следует, в частности, иметь в виду, что достигнутая ныне полная отчётливость и законченность теории бесконечно больших и бесконечно малых переменных величин заключается лишь в сведении всех трудностей этой теории к вопросу обоснования учения о числе, в которое существенно входит представление о Б. системы чисел. Утверждение о том, что у бесконечно мало, имеет смысл только при указании характера изменения у в зависимости от какого-либо другого переменного х; например, говорят, что у бесконечно мало при х ® а, если при любом e > 0 существует такое d > 0, что из |х — a| < d вытекает |у| < e. В самое это определение уже входит предположение, что функция y = f (x) определена для бесконечного множества значений х (например, для всех действительных х, достаточно близких к а). О бесконечных множествах в математике подробнее см. Множеств теория.
В теории множеств терминам «актуальная» и «потенциальная» Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности «актуально бесконечным числом». Дело в том, что бесконечные системы математических объектов (например, натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо «образовал» множество натуральных чисел, перечислив их фактически «все» одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к n + 1. В случае континуума действительных чисел уже рассмотрение одного его элемента ‒ действительного числа ‒ приводит к изучению процесса образования его последовательных приближённых значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуумы), может характеризоваться как Б. лишь «потенциальная». Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как «актуально» заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, ещё нельзя считать законченным. См. Множеств теория, Логика, Математика.
А. Н. Колмогоров.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Как вообразить несчетное множество? / Хабр
Как известно, бесконечности бывают разных типов. Бывают счетные, бывают несчетные. Несчетные делятся на множества мощности континуум и все остальные. Счетные множества это такие, элементы которых можно упорядочить в длинный ряд и занумеровать натуральными числами. С несчетными такой фокус не удается. Тогда как же можно представить несчетное множество, в частности множество вещественных чисел [0;1)? Ответ — дерево бесконечной высоты.
Для меня несчетные множества всегда выглядели как непонятное, туманное облако символов витающее где-то на задворках мозга. Но вот недавно
облако скондесировалось в пару не слишком аккуратных, но компактных кристаллов. О них собственно и речь.
Чтобы избежать путаницы, под несчетным множеством будем подразумевать множество мощности континуум (к таким относятся вещественные числа, иррациональные числа, множество всех подмножеств натуральных чисел и другие).
Карусель
Как известно из википедии и других достоверных источников, мощность вещественных чисел отрезка [0;1) является континуумом. Вещественные числа из этого отрезка нельзя посчитать натуральными числами, т.е. сделать так чтобы одному натуральному числу соответствовало одно вещественное и наоборот. Для неверующих проведем диагональную процедуру Кантора.
Представим чисела отрезка [0,1) в двоичной системе счисления и получим набор бесконечных последовательностей единиц и нулей.
Допустим, мы упорядочили такой набор в виде бесконечного списка как на рисунке. Упорядочив, получим квадратную таблицу в каждой ячейке которой находится либо 1, либо 0. Рассмотрим ячейки располагающиеса на главной диагонали.
Инвертировав диагональ(000010…) получим последовательность не попадающую в наш список, так как полученная последовательнось отличается от каждой попавшей в список хотя бы одним элементом. Последовательность номер n будет отличаться от диагональной в n-ой позиции. Следовательно, диагональная последовательность отсутствует в списке.
Исходя из приведенной схемы несчетное множество можно представлять в виде непрерывногенерируемых последовательностей. Инвертировали одну диагональную последовательность — вставили её в начало списка — сгенерировали новую и так далее. Такая карусель выглядит сомнительно.
Дерево
Давайте теперь посмотрим на двоичное, дерево что на следующем рисунке. Корень, наследники. В правом наследнике каждого узла — 1, в левом -0. Множество путей в дереве — пути от корня до каждого из листьев. Для дерева высоты N множество максимальных путей от вершины до листьев будет соответствовать множеству всех последовательностей нулей и единиц длинны N, даже если N — бесконечность.
Допустим нашлась последовательность не входящая в дерево. Попробуем наложить её на один из путей дерева: 0,1,0,1 … в какой-то момент должна найтись такая развилка в которую наша последовательность не укладывается. Но из каждого узла дерева выходят либо 0, либо 1, поэтому чтобы не уложиться в путь на дереве последовательность должна содержать элементы отличающиеся от 0 или 1.
Получается, множество максимальных путей в бинарном дереве бесконечной высоты имеет мощность континуум, что эквивалентно мощности вещественных чисел отрезка [0;1).
Если вернуться к интерпретации бинарных последовательностей как двоичных дробей, то рациональные дроби вида 0,x(y) будут выглядеть в виде конечной кривулины х и бесконечной последовательности кривулин y, иррациональные числа будут выглядеть как одна бесконечная неповторяющаяся кривулина x.
Смешная загогулина
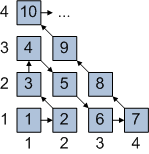
В полученном результате есть одна загвоздка: Количество путей максимальной длинны, исходящих из корня двоичного дерева бесконечной высоты несчетно. Количество же вершин такого дерева можно посчитать. Это легко сделать последовательно нумеруя вершины сверху вниз.
Для дерева конечной высоты расклад другой:
Количество путей максимальной длинны, исходящих из корня в двоичном дереве высотой N равно 2^(N-1), а количество вершин почти в два раза больше — 2^N — 1. Устремляя N к бесконечности получим, что счетная бесконечность вершин в два раза “больше” несчетной бесконечности путей.
Вот такой псевдопарадокс, иллюстрирующий работу интуиции.
Эффективной интуиции нам всем :).
Самое интересное в теории множеств то, что она рассматривает не только конечные множества – множества, содержащие конечное число элементов, но и бесконечные, для которых даже понятие числа бессмысленно. То есть, теория множеств может рассматривать не только множество студентов в группе и множество березок в лесу, но и множество точек на прямой, и множество звезд на небе…
Основоположник теории множеств Георг Кантор именно из‑за бесконечности попортил себе много крови, да так крепко попортил, что пришлось подключаться врачам‑психиатрам. Хотя с бесконечностью математики до него уже давным‑давно работали. Взять то же бесконечно большое множество точек на прямой или наоборот, бесконечно малые величины из высшей математики…
Но вся беда в том, что ни один живой человек не видел, не слышал, не щупал бесконечности! Поэтому до Кантора математики признавали и использовали так называемую ПОТЕНЦИАЛЬНУЮ бесконечность. Самый кондовый пример – это понятие бесконечно большого числа в высшей математике. Бесконечно большое число это число, которое больше любого наперед заданного. Если человек не понимает, о чем речь, то его просят назвать самое большое число в мире!… Образованный человек обычно называет число миллиардмиллиардов. А ему об’ясняют, что бесконечно большое число больше этого числа – «даже больше чем на еще миллиардмиллиардов».
То есть у нас с вами всегда в запасе есть число потенциально(! ) большее, чем придумает эрудит…
Кантор же позволил себе в математике АКТУАЛЬНУЮ бесконечность. То есть то, что до этого могли позволить себе лишь поэты, с которых, как известно, никто строго не спросит… «звездам числа нет, бездне дна». Поэты не любят, чтобы по крохам, по каплям… Любят, чтоб сразу! «Вот она, ВСЯ бездна вашего падения!… Дарю тебе ВСЕ звезды – такой ничтожной малости, для тебя моя, бесценная‑единственная, не жалко!»… То есть по Кантору бесконечность существует сразу вся. А раз бесконечные множества есть, и сразу целиком, то с ними можно производить математические манипуляции. Их даже можно сравнивать на больше‑меньше.
Поэтому Кантор начал задавать себе «поэтические» вопросы и искать на них математические ответы. Один из ключевых вопросов: «БЕСКОНЕЧНО МНОГО – это всегда ОДИНАКОВО БЕСКОНЕЧНО МНОГО? Или могут быть большие и меньшие бесконечности? «
Чего больше, звезд на небе или точек на прямой?…
Кантор доказал великую теорему, из которой следует, что бесконечности могут быть разные по величине. Поскольку «число» и «количество» – слова в этом случае неуместные, то он ввел термин «мощность». Мощность – это то что остается, когда нас не интересует сущность элементов множества и порядок, в котором они располагаются. То есть, он определил понятие мощности строго, хотя определение и кажется на первый взгляд странным. На второй взгляд этого, обычно, так уже не кажется. От множества студентов останется только мощность, если мы перестанем их различать и будем воспринимать их вне всякого порядка (в естественных условиях).
Увы, приводить примеры множеств, имеющих бесконечную мощность, используя березки и студентов, не получится вообще, а звезды далеки и видны только ночью. Поэтому обратимся для наглядности к находящимся рядом с нами числам.
Пересчитывая что‑то мы используем целые (положительные) числа 1, 2, 3… Их еще называют «натуральными». Странные американцы любят начинать этот ряд с нуля (и заразили этим, например, всю вычислительную технику). Их не смущает, что «3‑блок» на самом деле 4‑ый по счету… Впрочем, нам сейчас все равно! При добавлении или удалении нуля ничего не меняется.
Главное, мы знаем, что чисел нам хватит для пересчета чего угодно. Мы также знаем, что это множество бесконечное. Кантор назвал это множество СЧЕТНЫМ и его мощность – мощностью счетного множества.
Мощность этого множества Кантор взял за эталон и стал сравнивать ее с мощностями других множеств.
Во‑первых, он установил, что эта мощность больше мощности любого конечного множества (студентов, березок и т.п.).
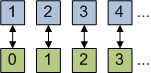
Во‑вторых, и это любопытно, он доказал, что многие бесконечные множества имеют ту же мощность (то же «количество» элементов), что и счетное. Один из самых поразительных примеров – это то, что множество целых положительных чисел имеет столько же элементов, сколько и множество целых четных положительных чисел! То есть они равномощны!
Действительно, запишем друг под другом:
1 2 3 4…
2 4 6 8…
Ясно, что обе последовательности имеют одинаковое количество элементов, поскольку любому числу первой, ВСЕГДА соответствует строго одно число второй последовательности. Так что вторая последовательность не может исчерпаться раньше первой. И наоборот!
Следовательно, эти множества равномощны!
Следовательно, здесь ЧАСТЬ РАВНА ЦЕЛОМУ !!!
Поскольку это доказано строго, то на последний спасительный аргумент – «так в жизни не бывает», можно еще раз, но уже более сурово ответить: «Вы просто жизни не видели! Точнее, вы никогда не видели в жизни бесконечность! И не увидите!». За свою непростую долгую жизнь человек может столкнуться даже с паровозом, а с бесконечностью – никогда! Даже в темноте.
Поэтому, что может быть и чего не может быть в мире бесконечностей не нам судить, основываясь лишь на житейском опыте!
Из бесконечного множества звезд (мощность которого тоже счетна) мы видим лишь их ограниченное конечное множество. На нарисованном отрезке прямой, содержащем бесконечное множество точек, мы видим конечное множество зерен грифеля, которым отрезок нарисован. Кстати, мы видим все это и многое другое сетчаткой глаза, содержащей конечное число палочек‑колбочек. Конечным числом палочек‑колбочек своего глаза никогда ничего бесконечного вы не увидите!…
Так что бесконечности вокруг нас существуют в «параллельном мире» по своим законам, которые теория множеств помогает изучать.
Мы уже сказали «во‑вторых», но есть еще и «в‑третьих» – и это в‑третьих» – самое главное: великая теорема Кантора, которая уже упоминалась.
Дело в том, что если построить множество всех подмножеств конкретного множества, то всегда получите множество БОЛЬШЕ исходного.
Например, возьмем множество из 2‑х элементов: РАЗ, ДВА (и обчелся). Подмножествами этого множества будут 4 множества(!):
1) РАЗ, ДВА – (любое множество подмножество самого себя)
2) РАЗ
3) ДВА
4) пустое – (т.е. «обчелся»).
Другой пример: А И Б (сидели на трубе)
Подмножествами этого множества из трех элементов будет 8 множеств:
1) А, И, Б
2) А, И
3) А, Б
4) И, Б
5) А
6) И
7) Б
8) пустое
Из четырех элементов получилось бы 16 элементов. И этот ряд можно бесконечно продолжить, как ряд степеней числа 2.
Так вот, Кантор и доказал, что если взять бесконечное множества счетной мощности, например, множество целых положительных чисел и построить (разумеется, умозрительно) множество, содержащее в качестве элементов все подмножества этого множества, то получим мощность БОЛЬШУЮ , чем счетная мощность. В принципе не существует способа пересчитать (пусть в бесконечности) такое множество. В нем всегда больше элементов. Эта новая большая мощность называется мощностью КОНТИНУУМА .
И снова житейский парадокс. Мощность континуума имеет, например, множество точек прямой или множество действительных чисел, что то же самое. Более того, любой отрезок числовой оси, даже такой малюсенький отрезок, как отрезок от 0 до 1, имеет мощность континуума, то есть на нем больше чисел, чем найдется чисел в счетном множестве. А раз этот отрезок имеет мощность континуума, как и вся (бесконечная) прямая и, естественно, любой ее отрезок, то можно сказать, что на отрезке от 0 до 1 ровно столько же точек, сколько на отрезке прямой от Земли до Юпитера.
Здесь тоже часть равна целому, если и часть, и целое имеют мощность континуума. И все они одинаково больше числа звезд на небе или числа всевозможных алгоритмов…
Для бесконечностей существует очень простая арифметика, которая логически следует из предыдущих разговоров. Сложение двух счетных мощностей дает счетную мощность, а для континуумов – мощность континуума. При вычитании из мощности континуума счетной – в остатке мощность континуума. Но вот если вычитать из континуума континуум или из счетной мощности счетную – всякое может получиться в каждом конкретном случае. Тут запросто можно напрячься и придумать свои иллюстрации.
Однако, не все так просто. Бесконечность остается одной из ключевых категорий философии. И математика здесь подливает масла в огонь, показывая все новые грани этой проблемы. Тем более, если говорить не только о бесконечных, но и о бесконечных упорядоченных множествах. Впрочем, желающие могут почитать книжки об очень красивых вещах с немение красивыми романтическими названиями: «кардиналы и ординалы».
Что такое бесконечность?
Статья посвящена поиску ответа на вопрос, что такое бесконечность? Наверняка, многих мучает этот вопрос, так что же такое бесконечность? Какой смысл у этого слова? Я тоже задумывалась над этим вопросом и попыталась найти на него ответ. Ведь, бесконечность может быть в виде математического знака восьмерки, или же эта вселенная у которой нет конца и начала. Надеюсь, после прочтения статьи, вы сможете понять значения этого слова, которое волнует каждого человека.
Как в философии появилась бесконечность?
Философия, говоря по определению, как бы сфера плюральности. Философия возможно больше исследует, чем действительное. В этом ее блеск и нищета. Бесконечность появилась уже не из философской сферы, а религиозной. Потому что актуальная бесконечность пришла в европейскую мысль, когда произошло обращение Европы к христианству, пришла ближневосточная культура, библейские предсказания о Боге, монотеизм. То есть Бог бесконечен, бесконечно мудрый, Бог есть бесконечно милостивый (в христианском богословии). Для античности Бог был конечен, вот тогда и начались попытки осмыслить это философии. (Программа Александра Гордона «Осознание и признание бесконечности. Что собой представляет эта величина?»; 2016-04-17)
Термин бесконечность соответствует нескольким различным понятиям, в зависимости от области применения, будь то математика, философия, или повседневная жизнь. Бесконечность появилась как абстрактное количественное обозначение чего-то непостижимо большого, в применении к сущностям без пространственных или временных границ. (Доклад профессора, доктора философских наук Кармина Анатолия Соломонович; 2016-04-17)
Как заметил Аристотель, мышление человеческое – это вещь особенная. Оно, как он пишет, не останавливается, то есть мышление не может остановится. Вы сказали один, два, три, пошли дальше. На три нельзя остановиться должно быть что-то четверное, то есть принцип математической индукции. Где граница? Мы не можем досчитать до бесконечности, к примеру до миллиона, но это займет очень много времени. Если мы оборвем счет, то мы будем знать, что оборвали счет. На самом деле можно считать дальше. Отсюда возникает понятие, которое уже носит математический характер, потенциальная бесконечность.
Потенциальная бесконечность – бесконечно продолжающийся процесс. Например, бесконечное число рядов, бесконечная линия, прямая линия в геометрии.
Затем философы стали думать о том, а нет ли такой бесконечности, которая была бы действительно неограниченна, то есть не имела бы никакой границы в реальности. Это Бог. Бог – это все, все создано богом. Если Бог это все, то его нельзя определить, то есть Бог не имеет никаких пределов, границ не потому, что он практически бесконечен, он теоретически бесконечен. Но как он бесконечен? У него, что потенциальная бесконечность? Он актуально бесконечен.
Понятие актуально бесконечен впервые появилось в философии, то есть какая-то субстанция. Есть конечный мир, а есть бесконечное что-то за пределами нашего мира – трансцендентное.
Вселенная актуально бесконечна в математическом смысле. Если провести прямую линию от земли куда-то в даль, она вся отдана вселенной со своей бесконечностью. А если в вселенная может продолжаться и расширятся, то она потенциально бесконечна. Как устроена вселенная? Вселенная – бесконечное пространство, она трех мерна. (Доклад профессора, доктора философских наук Кармина Анатолия Соломоновича; 2016-04-17)
Также бесконечность неразрывно связана с обозначением бесконечно малого, к примеру, ещё Аристотель сказал:
«… всегда возможно придумать большее число, потому что количество частей, на которые можно разделить отрезок, не имеет предела. Поэтому бесконечность потенциальна, никогда не действительна; какое бы число делений не задали, всегда потенциально можно поделить на большее число. «
Бесконечность изменяется во времени, но всему этому есть логика. Например, человеческим открытиям, знаниям и бесконечность тоже развивается логически.
Если заглянуть в древнюю философию, то категория бесконечности вообще не отличалась от категории неопределенности. Можно сделать вывод, что бесконечность – это нечто неопределенное. Именно так, слово бесконечность понималось в древности. Отсюда возникло понятие, понятие практическая бесконечность, то есть мы считаем бесконечным то, что практически для нас не имеет видимых границ. Например, у А.С. Пушкина «Евгений Онегин»:
«И бесконечный котильон
Ее томил, как тяжкий сон.»
(Доклад профессора, доктора философских наук Кармина Анатолия Соломоновича; 2016-04-17)
То есть бесконечность – нечто большое, бесконечное.
Как бесконечность стала предметом точной науки?
Если посмотреть на математику XIX века, она представляла собой конфедерацию математических теорий, каждая их которых формировала свой взгляд на бесконечное. Скажем, геометрия, в ней было бесконечное перечисление параллельных прямых, в анализе – это были бесконечно большие или бесконечно малые величины. Но общим подходом было то, что математика в целом понимала бесконечность, как нечто отрицательное, нечто противоположное в конечному. (Программа Александра Гордона «Осознание и признание бесконечности. Что собой представляет эта величина?»; 2016-04-17)
Понятие бесконечности в физике и математике
Рассматривая различные случаи использования понятия бесконечности в науке, нельзя не заметить, что смысл этого понятия меняется в зависимости от обстоятельства, в которых оно употребляется.
В физике бесконечным считается то, что по отношению к изучаемым явлениям чрезвычайно велико или чрезвычайно мало. Например, при изучении движения тел около земной поверхности можно считать расстояние от Земли до Солнца бесконечно большим и соответственно действие солнечного тяготения на них бесконечно малым. Как справедливо отмечает Г. И. Наан, «во всех физических задачах бесконечность означает просто «достаточно далеко». Это могут быть и парсеки (в астрономии), и километры или метры (в электродинамике), и даже миллиардные и значительно меньшие доли сантиметра в теории атомного ядра». (Г. И. Наан Общие вопросы космологии «Труды шестого совещания по вопросам космогонии», Изд в АН СССР, 1959, 256 с.)
Тем самым бесконечность выступает здесь как бесконечное лишь в строго определенном отношении, будучи в других отношениях конечным.
Понимаемую таким образом бесконечность можно назвать «физической» бесконечностью. «Физическая» бесконечность позволяет получать ценные научные выводы, достаточно строгие и точные.
«Физическая» бесконечность – научная абстракция, с помощью которой мы получаем возможность выразить определенные, объективно существующие отношения между вещами. Но она отражает эти отношения односторонне, упрощенно. Поэтому в каждом конкретном случае область ее использования ограничена.
В отличии от абстракции «физической» бесконечности математическое понимание бесконечного выступает, как абстракция «более высокого ранга». (Кармин А. С. Постановка проблемы бесконечности в современной науки. Ленинград, 1965, 124 с.)
Различают два основных вида математической бесконечности: потенциальная и актуальная. Первая, как я уже сказала выше, означает неограниченно продолжающийся процесс, вторая – актуально, налично существующую в виде завершенного целого бесконечную величину. С помощью этих абстракций в различных разделах математики создаются разные математические образы бесконечного. Математическая бесконечность начинает тогда казаться образцом, которому, как идеалу, должна следовать природа. Однако реальная бесконечность природы не должна обязательно подчиняться нашим математическим представлениям о бесконечности. «Идеальная потребность математика вовсе не есть принудительный закон для реального мира» (Ф. Энгельс. Анти-Дюринг. Госполитиздат, 1953, стр. 49).
Бесконечность в математике принимается как число количественная определенность, как бесконечное количество. Но количество «вообще», количество как таковое, безотносительно к качественной определённости есть абстракция. В реальном мире в отличии от мира абстракции количество всегда есть количество какого-то качества. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 124 с.)
Значит, математические абстракции бесконечности имеют реальный смысл лишь как выражение бесконечного количества некоего качества. Но в природе все имеет меру, и всякое качество связано с определенными границами присуще ему количественных изменений.
Как мы вообще приходим к понятию бесконечности?
Допустим, что мы начинаем считать, двигаясь по натуральному ряду чисел. Можно ли путем такого движения и счета получить понятие бесконечности, т. е. можно ли дойти до такого числа, которое необходимо было бы назвать бесконечным? Конечно, нельзя. Сколько бы мы ни двигались по натуральному ряду чисел, мы никогда не дойдем до бесконечности. Следовательно, целых чисел мало для конструкции понятия бесконечности; тут нужны совсем другие подходы.
Если не хватает натурального ряда чисел, возьмем числовое инобытие и посмотрим, не встретим ли мы здесь категорию бесконечного числа. Однако, что такое инобытие? Инобытие числа, если его брать в чистом виде, во всем абсолютно противоположно числу: число есть четкая раздельность, инобытие числа–сплошная неразличимость; число – устойчивость и прерывность, числовое инобытие – неуловимая подвижность и алогическая непрерывность. В таком виде взятое, числовое инобытие никакого отношения к бесконечности не имеет.
Бесконечность прежде всего есть нечто; сущность же инобытия заключается именно в том, что оно не есть нечто (иначе оно было бы бытием, а не инобытием), а существует оно всегда только в отношении числа и бытия. О числовом инобытие нельзя ни того, что он конечен, ни того, что он бесконечен. Об инобытии, если его брать в чистом виде, невозможно никакое утверждение. Оно живет именно размывом и становлением. Таким образом, бесконечного числа на этом пути мы не можем достигнуть. Тут повторяется, собственно говоря, то же бессилие, что и в случае с целым числом. В крайнем случае чистое инобытие приводит к беспредельному становлению, при котором ни о какой новой точке становления нельзя сказать, что эта точка бесконечно удалена от начала становления. Инобытие делает как бы бессильный жест в сторону бесконечности, но не дает самой бесконечности. (Лосев А.Ф. Хаос и Структура. – Москва «Мысль», 1997, 495-496 с.)
О сказанном выше, я задаюсь вопросом, есть ли такое состояние мысли – мысль о бесконечности? Мне кажется, что нет. Это, как и движение по натуральному ряду чисел, есть не конструкция бесконечности, а лишь бессильный жест в сторону бесконечности и полная невозможность сказать о ней что-нибудь положительное.
Бесконечность как философская категория
В наиболее широком смысле понятие бесконечности использует философия. Действительно, диалектический материализм рассматривает бесконечность как ее атрибут.
Рассматривая бесконечность в наиболее широком плане, диалектика материалистическая философия получает возможность выделить то наиболее общее и существенное, что характеризует бесконечность, как атрибут материи и что как или иначе лежит в основе всех научных представлений о ней, поскольку все они являются в конечном счете представлениями об одном и том же. Таким образом, научно философское, диалектик материалистическое понимание бесконечности может рассматривать как обобщение различных абстракций бесконечности, используемых в науке.
Категория бесконечности тесно связана с категориями абсолютного и относительного. Абсолютное и относительное в материальном мире образует нереальное единство. Любые конкретные процессы, состояния, свойства, качества материи являются относительными. Но в их постоянном движении, изменении, превращении выявляется абсолютное.
Бесконечность обнаруживается нами всегда и выступает как форма проявления абсолютного. Признание бесконечности материи, движения, пространства и времени следует именно из признания их абсолютности. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 125 с.)
Таким образом, абсолютное существует не само по себе «в чистом виде», а лишь через относительное. Однако, появляясь в относительности, абсолютное не может быть сведено к нему. Эта противоречивая взаимосвязь и выражается категорией бесконечности. Бесконечность представляет собой не что иное, как способ разрешения противоречия между абсолютным и относительным, способ из взаимного перехода друг в друга.
Особенности постановки проблемы бесконечности в философии и естественных теориях
Как я уже говорила, существует некоторое различие между употреблением понятия абсолютности в философии и его употреблением в естественных теориях.
Философия рассматривает понятие абсолютности в самом общем значении, считая абсолютным лишь то, что непреложно всеобще для мира «в целом», для материи «вообще». В философском понимании абсолютны лишь наиболее общие законы и атрибуты бытия: например, движение, пространство и время, закон перехода количественных изменений в качественные.
Любой естественнонаучный закон в этом более узком смысле абсолютен, ибо иначе он вообще не был бы законом. Каждая конкретная научная теория, имея перед собой всегда определенную конкретную область исследования, считает абсолютным то, что непреложно в данной области, то есть то, сто абсолютно не «вообще», а лишь в отмеченном более узком смысле.
Ясно, что это абсолютное за пределами данной области действительности является относительным. Однако то, что одно и то же может выступать в одном отношении как абсолютное, а в другом как относительное, — это объективный факт. Например, то, что вода закипает при 100°С – это абсолютный, всеобщий закон природы. Но в то же время, будучи зависимым от условий, которые могут быть, а могут и не быть, этот закон оказывается относительным. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 126 с.)
Таким образом, он и абсолютен и относителен, и это не смешение понятий, а отражение диалектической противоречивости объективного мира.
Следовательно, в отличии от философии, понятие абсолютного в рамках всякой естественнонаучной теории есть абстракция. Эта абстракция нужна и полезна, но она теряет силу тогда, когда невозможно отвлечься от изменения данных условий и приходится учитывать новые, иные условия.
Реальная бесконечность природы есть выражение ее абсолютного характера – абсолютного в самом полном и широком смысле слова. Так как в философии речь идет именно об «абсолютном в общем», «безусловно абсолютном», то она вырабатывает наиболее общие понятия бесконечности, отражающие реальную конечность природы в общем виде.
В естественнонаучных теориях понятие бесконечности тоже употребляется как выражение абсолютного его соотношении с относительным. Но абсолютное тут понимается не как «абсолютное вообще», а как «абсолютное при определенных условиях», и поэтому бесконечность выступает тоже не как реальная бесконечность вообще, а как бесконечность при определенных условиях. Бесконечность конкретных свойств и состоянии материи – это не реальная бесконечность. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 127 с.)
Таким образом, наиболее общая постановка проблемы бесконечности дает только философия. Поскольку она относится к конкретным свойствам и состояниям материи, а не ко всей материи вообще.
Бесконечность пространства
Если говорить о пространстве вообще как универсальной форме существования материи, то оно выступает как абсолютное в самом широком смысле. Как говорилось выше, что это абсолютное пространство бесконечно, и бесконечность его есть реальная бесконечностью.
Но если речь идет о физическом пространстве – о пространстве, окружающем нас и обладающем определенной, свойственной ему структурой, — то оно не является «абсолютным вообще».
Значит, то конкретное физическое пространство, которое изучается естественными науками, не бесконечно. Бесконечность есть его научная абстракция, и когда в естествознании говорится о бесконечности пространства, то обычно имеется в виду не реальная бесконечность, а именно эта абстракция. Она основана на абсолютизации пространства и поэтому носит характер «дурной» бесконечности. Она полезна и даже необходима, но ее нельзя принимать за реальную бесконечность пространства. Сфера применяемой этой абстракции ограничена. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 127 с.)
Исходя из этого можно сказать, что на некотором этапе развития науки, когда придется рассматривать пространство в новых отношениях и перед ними раскроются новые, более общие свойства и формы его, тогда ограниченность абстракции будет обнаружена и мы столкнемся с необходимостью считать «наше» физическое пространство конечным.
Парадокс обнаруженный А. Л. Зельмановым, находит рациональное объяснение, что не инвариантность бесконечности, то есть «дурная» пространственная бесконечность – это относительность бесконечности конкретного определенного физического пространства. Значит, о бесконечности можно говорить только в определенных отношениях, абстрагируясь от других отношений, в которых оно является конечным.
Также находит подтверждение в исследованиях А. З. Петрова о том, что реальная бесконечность пространства гораздо сложнее, чем «дурная» бесконечность. Она важна не только в физических, но и философских отношениях. Путем анализа алгебраической структуры уравнений Эйнштейна А. З. Петров показал, что имеются три различных типа пространства. Но если в бесконечной Вселенной имеются пространства различных типов, то «дурная» бесконечность становится бессмысленной.
Если в этих условиях реальная бесконечность пространства отожествляется с его «дурной» бесконечностью, то невозможно считать пространство бесконечным. Это, вероятно, послужило причиной того, что некоторые ученые, стоящие на позициях диалектического материализма, стали пытаться вообще пересмотреть положение марксистской философии о бесконечности пространства. Например, Э. Кольман.
В статье «Современная физика в поисках дальнейшей фундаментальной теории» Э. Кольман считает, что «если только математика, физика, космология низведут – каждая у себя – понятие бесконечности до вспомогательного понятия, до абстрактной экстраполяции, то понятие бесконечности не сможет в философии сохранить свое прежнее положение». («Вопросы философии», 1965, №2, стр. 119) Но, во-первых, Э. Кольман сам признает необходимость использовать это понятие, говоря о бесконечном многообразии материи и бесконечных изменениях ее, то есть считает бесконечность атрибутом материи, а во-вторых, если бесконечность все же является атрибутом материи, то приходится признать необходимость философской категории бесконечности, которая выражает то общее и существенное, что лежит в основе научных абстракций бесконечности. Ограниченность этих абстракций обусловлена тем, что бесконечности вообще нет, а тем, что они являются односторонними, упрощёнными образами ее. Мысль Э. Кольмана верна в том смысле, что философское понятие бесконечности нельзя сводить к «дурной» бесконечности или тому подобной «абстрактной экстраполяции», что философия должна дать более глубокое понятие бесконечности. (Кармин А. С. Постановка проблемы бесконечности в современной науки. — Ленинград, 1965, 128-129 с.
В заключении хочу сказать, что бесконечность или бесконечное столь же познаваемо, как и непознаваемо, и раскрытие его сущности может происходить лишь в виде «бесконечного асимптотического прогресса» (по положению Энгельса), то есть все атрибуты и законы материи оказываются одновременно специфическими и частными для всего мира, например, пространство, время, движение, системность. Когда мы говорим о том, что мир есть единое связное целое, то можно определить, что здесь подразумевается понятие «целое». Поскольку Вселенная бесконечна, то о ней нельзя говорить, как о какой-то замкнутой системе, иначе говоря какую бы конкретную систему любого порядка и масштабов мы ни взяли, она будет входить во Вселенную. По моему суждению, во Вселенной нет единого количественного закона развития всех систем, а положение во Вселенной как едином связном целом означает лишь признание материального единства мир (то есть общность материи, как некой субстанции, как носителя многообразных свойств и отношений), подчинение всех объектов тем всеобщим законам, которые исследуются диалектическим материализмом. А диалектический материализм в свою очередь это система взглядов на окружающий мир.
Бесконечность является абстрактным понятием, используемым, чтобы описать или обозначить нечто бесконечное или безграничное. Это понятие важно для математики, астрофизики, физики, философии, логики и искусства.
Вот несколько удивительных фактов об этом комплексном понятии, которые способны взорвать мозг лбого человека, не очень близко знакомого с математикой.
Символ бесконечности
У бесконечности есть свой собственный специальный символ: ∞. Символ, или лемниската, был введен священнослужителем и математиком Джоном Уоллисом в 1655 году. Слово «лемниската» происходит от латинского слова lemniscus, что означает «лента».
Уоллис, возможно, основал символ бесконечности на римской цифре 1000, рядом с которой римляне раньше указывали «бесчисленный», в дополнение к числу. Также возможно, что символ основан на омеге (Ω или ω), последней букве греческого алфавита.
Интересный факт заклчается в том, что понятие бесконечности появилось и использовалось задолго до того, как Уоллис наградил его символом, который мы используем по сей день.
В четвертом веке до нашей эры джайнистский математический текст под названием Сурья-праджнапти-сутра разделял все числа на три категории, каждая из которых, в свою очередь, разделялась на три подкатегории. В этих категориях были указаны перечислимые, неперечислимые и бесконечные числа.
Апория Зенона
Зенон Элейский, родившийся приблизительно в пятом веке до н. э., был известен парадоксами, или апориями, включающими и понятие бесконечности.
Из всех парадоксов Зенона самым известным является «Ахиллес и Черепаха». В апории черепаха бросает вызов греческому герою Ахиллесу, приглашая его на гонку. Черепаха утверждает, что выиграет гонку, если Ахиллес даст ей преимущество в тысячу шагов. Согласно парадоксу, за то время, что Ахиллес пробежит все расстояние, черепаха сделает в ту же сторону еще сто шагов. Пока Ахиллес пробежит еще сто шагов, черепаха успеет сделать еще десять и так далее по убывающей.
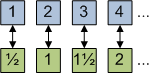
В более простом изложении парадокс рассматривается так: попробуйте пересечь комнату, если каждый следующий шаг в половину меньше предыдущего. Хоть каждый шаг и приближает вас к краю комнаты, вы никогда на самом деле не доберетесь до него, или доберетесь, но на это потребуется бесконечное количество шагов.
Согласно одной из современных трактовок, этот парадокс основан на ложном представлении о бесконечной делимости времени и пространства.
Число пи – пример бесконечности
Отличным примером бесконечности является число пи. Математики используют для числа пи символ, потому что невозможно записать все число целиком. Пи состоит из бесконечного количества чисел. Оно часто округляется до 3,14 или даже 3,14159, но неважно, сколько цифр записано после запятой, ведь невозможно добраться до конца числа.
Теорема о бесконечных обезьянах
Еще один способ думать о бесконечности – рассмотреть теорему о бесконечных обезьянах. Согласно теореме, если дать обезьяне печатную машинку и бесконечное количество времени, в конечном счете у обезьяны получится напечатать «Гамлета» или любое другое произведение.
В то время как многие люди воспринимают теорему как демонстрацию веры в то, что нет ничего невозможного, математики рассматривают ее как доказательство невозможности определенного события.
Фракталы и бесконечность
Фрактал – это абстрактный математический объект, используемый в математике и искусстве, чаще всего он моделирует природные явления. Фрактал записывается как математическое уравнение. Рассматривая фрактал, можно заметить его сложную структуру на любом масштабе. Другими словами, фрактал бесконечно увеличиваем.
Снежинка Коха является интересным примером фрактала. Снежинка выглядит как равносторонний треугольник, образующий замкнутую кривую бесконечной длины. Увеличивая кривую, на ней можно увидеть все новые и новые детали. Процесс увеличения кривой может продолжаться бесконечное количество раз. Несмотря на то что у снежинки Коха есть ограниченная область, она ограниченна бесконечно длинной линией.
Бесконечность разных размеров
Бесконечность безгранична, на все же она поддается измерению, пусть и сравнительному. Положительные числа (больше 0) и отрицательные числа (меньше 0) могут похвастать бесконечными наборами чисел равных размеров. А что происходит, если объединить оба набора? Получится вдвое большой набор. Или еще пример – все четные числа (их бесконечное количество). И все равно это всего лишь половина бесконечного количества всех целых чисел. Другой пример, просто прибавьте единицу к бесконечности. Поучится число на 1 больше бесконечности.
Космология и бесконечность
Космологи изучают Вселенную, неудивительно, что понятие бесконечности играет для них важную роль. Есть ли границы у Вселенной или она бесконечна?
Этот вопрос до сих пор остается без ответа. Наша Вселенная расширяется, но куда? И где предел этого расширения? Даже если у физической Вселенной и существуют границы, у нас все еще есть теория мультивселенной, которая рассматривает существование бесконечного количества Вселенных, в которых могут быть отличные от нашей законы физики.
Деление на ноль
Деления на ноль не существует. Оно невозможно, по крайней мере, в обычной математике. В привычной нам математике единицу, поделенную на ноль, невозможно определить. Это ошибка. Однако так бывает не всегда. В расширенной теории комплексных чисел деление единицы на ноль не вызывает неминуемого коллапса и определяется некоторой формой бесконечности. Другими словами, математика бывает разной, и не вся она ограничивается правилами из учебников.
Нашли нарушение? Пожаловаться на содержание
Две монументальных работы убедили многих математиков отказаться от знака равенства. Их цель – реконструировать основы дисциплины при помощи более слабого взаимоотношения – «эквивалентности». И этот процесс не всегда идёт гладко.
Знак равенства – краеугольный камень математики. Он, кажется, делает фундаментальное и непротиворечивое заявление: две этих сущности абсолютно одинаковы.
Однако ширится круг математиков, относящихся к знаку равенства, как к первоначальной ошибке математики. Они считают его внешним лоском, прячущим важные сложности взаимоотношения величин – сложности, способные открыть решения огромного количества задач. Они хотят реформировать математику, используя более свободный язык эквивалентности.
«Мы породили эту идею равенства, — сказал Джонатан Кэмпбелл из Университета Дьюка. – А на её месте должна была быть эквивалентность».
Наиболее выдающейся фигурой этого сообщества является Джейкоб Лурье. В июле 41-летний Лурье покинул свой пост штатного сотрудника в Гарварде ради факультетской должности в Институте передовых исследований в Принстоне, где работали одни из самых выдающихся математиков мира.
Идеи такого масштаба, как у Лурье, редко встретишь в любой области. В своих книгах, растянувшихся на тысячи насыщенных техническими подробностями страниц, он создал удивительно отличный от обычного способ понимания самых основных концепций математики, выйдя за рамки знака равенства. «Думаю, ему казалось, что это правильный способ мышления о математике», — сказал Майкл Хопкинс, математик из Гарварда и руководитель в аспирантуре.
Первую свою книгу, «Теория высшего топоса», он опубликовал в 2009. 944-страничный том служит инструкцией по интерпретации признанных областей математики на новом языке » категорий бесконечности». В последующие годы идеи Лурье проникли в широкий спектр математических дисциплин. Многие математики считают их незаменимыми для будущего этой области. «Никто уже не будет прежним, изучив категории бесконечности», — сказал Джон Фрэнсис из Северо-Западного университета,
Джейкоб Лурье
Однако распространение категорий бесконечности вскрыло все проблемы, через которые проходит уважаемая область математики, пытаясь впитать новые смелые идеи – особенно такую идею, которая бросает вызов самой важной её концепции. «В математическом сообществе существует определённый уровень консервативности, — сказал Кларк Барвик из Эдинбургского университета. – Не думаю, что от любой группы математиков можно ожидать быстрого принятия любого инструмента без убедительных причин».
Хотя многие математики приняли категории бесконечности, мало кто из них прочёл длинные и чрезвычайно абстрактные тексты Лурье целиком. В итоге часть основанных на его идеях работ оказывается менее строгой, чем принято в математике.
«Я слышала, как говорят: ’Это есть где-то у Лурье’, — сказала Инна Захаревич, математик из Корнелловского университета. – А я говорю: ’Правда? Вы же ссылаетесь на 8 000 страниц текста’. Это не ссылка, это апелляция к авторитету».
Математики всё ещё пытаются осознать как широту идей Лурье, так и уникальный способ их представления. Они извлекают суть его презентации категорий бесконечностии подают его в новой упаковке так, чтобы ими могли воспользоваться больше математиков. В каком-то смысле они выполняют необходимое руководство, которое обязано следовать за любой революцией, переводя революционный текст в повседневный свод законов. Тем самым они создают будущее математиков, основывающееся не на равенство, а на эквивалентность.
Бесконечные башни эквивалентности
Математическое равенство кажется наименее противоречивой из всех идей. Две бусинки плюс одна бусинка равняются трём бусинкам. О чём тут ещё говорить? Однако самые простые идеи могут быть самыми обманчивыми.
С конца XIX века основы математики строились на наборах объектов, именуемых множествами. Теория множеств задаёт правила, или аксиому, по созданию и обращению с этими множествами. Одна из этих аксиом, к примеру, утверждает, что ко множеству из двух элементов можно добавить множество из одного элемента, и получить новое множество из трёх элементов: 2 + 1 = 3.
Формальный способ продемонстрировать равенство двух величин заключается в том, чтобы сопоставить пары друг другу. Сопоставьте одну бусинку справа от знака равенства с одной бусинкой слева. После всех сопоставлений лишних бусинок не останется.
Теория множеств признаёт, что два множества из трёх объектов каждое можно точно сопоставить друг другу, но не обозначает все различные возможные пути такого сопоставления. Первой бусинке справа можно подобрать пару в виде первой бусинки слева, или сопоставить первую справа со второй слева, и так далее (всего таких пар может быть шесть). Сказать, что два плюс один равняется трём, и закончить на этом – означает не увидеть всех возможных способов приравнять их. «Проблема в том, что способов составить пары много, — говорит Кэмпбелл. – И мы забываем их, когда говорим „равняется“».
Тут и вступает в игру эквивалентность. Если равенство является чётким взаимоотношением – две вещи либо равны, либо нет – эквивалентность может быть разной.
Когда вы точно сопоставляете каждый из элементов одного множества каждому элементу другого, вы получаете сильную эквивалентность. Но, к примеру, в такой области математики, как гомотопия, две формы (или геометрические фигуры) эквиваленты, если одну можно посредством растяжения или сжатия без разрывов превратить в другую.
С точки зрения теории гомотопии, плоский диск и точка в пространстве эквивалентны – диск можно сжать до точки. Однако сопоставить точки диска с точками точки нельзя. Ведь у диска точек бесконечное количество, а точка – это просто одна точка.
С середины XX века математики пытались выработать альтернативу теории множеств, в которой математикой было бы проще заниматься с точки зрения эквивалентности. В 1945 математики Сэмюель Эйлеберг и Сондерс Маклейн ввели новый фундаментальный объект со встроенной эквивалентностью. Они назвали его категорией.
Категорию можно наполнить чем угодно. Можно взять категорию млекопитающих, куда будут входить все волосатые теплокровные создания, вырабатывающие молоко. Или можно создавать категории математических объектов: множеств, геометрических фигур или числовых систем.
Категория – это множество с дополнительными метаданными: описанием всех способов сопоставления одного объекта другому, куда включено описание всех признаков, по которым два объекта могут считаться эквивалентными. Категории также можно представить себе в виде геометрических объектов, в которых каждый элемент категории представлен точкой.
Представьте, к примеру, поверхность шара. Каждая точка на этой поверхности может обозначать свой тип треугольников. Пути между точками выражают отношение эквивалентности между объектами. С точки зрения теории категорий мы забываем конкретный способ описания объекта и вместо этого концентрируемся на том, какое место занимает объект по отношению ко всем остальным объектам этого типа.
Каждая точка на поверхности соответствует определённому типу треугольников
«Мы относимся ко многим вещам, как к вещам, хотя реально они представляют собой взаимоотношение между вещами, — сказала Захаревич. – Фраза „мой муж“ обозначает нечто, что мы считаем объектом, но об этом можно думать и как о взаимоотношении. Определённая его часть определяется взаимоотношением со мной».
Версия категорий от Эйленберга и Маклейна хорошо подходила для работы с сильными вариантами эквивалентности. Но во второй половине XX века математики всё чаще использовали более слабые формы эквивалентности, такие, как гомотопия. «Математика становится более тонкой, и неизбежно у нас появляется стремление к более тонким идеям об обычных вещах», — сказала Эмили Рил, математик из Университета Джонса Хопкинса. У этих, более тонких вариантов эквивалентности, количество информации о взаимоотношениях двух объектов резко возрастает. Рудиментарные категории Эйленберга и Маклейна не были предназначены для такого.
Чтобы увидеть увеличение количества информации, сначала вспомните нашу сферу, обозначающую разные треугольники. Два треугольника гомотопно эквивалентны, если один можно превратить в другой растягиванием или иной деформацией. Две точки на поверхности гомотопно эквивалентны, если существует связывающий их путь. Изучая гомотопные пути между точками поверхности, на самом деле вы изучаете разные способы, которыми треугольники, обозначаемые этими точками, связаны друг с другом.
Однако недостаточно заявить, что две точки соединены многими равнозначными путями. Необходимо задуматься также и об эквивалентности всех этих путей. Поэтому кроме вопроса об эквивалентности точек, теперь вы задаёте вопрос об эквивалентности двух путей, начинающихся и заканчивающихся в одних и тех же точках – и есть ли путь, соединяющий эти пути. Этот путь, соединяющий пути, принимает форму диска, границей которого служат два этих пути.
Можно развивать эту идею и дальше. Два диска эквивалентны, если их соединяет путь – и этот путь примет форму трехмерного объекта. Такие трёхмерные объекты могут и сами быть соединены четырёхмерными путями (у пути между двумя объектами всегда на одно измерение больше, чем у самих объектов).
В итоге вы строите бесконечную башню эквивалентности между эквивалентностями. Рассуждая обо всей доктрине целиком, вы порождаете общий взгляд на все объекты, которые вы обозначили точками на сфере.
«Это всего лишь сфера, но оказывается, что для того, чтобы понять форму сферы, нужно в каком-то смысле уйти в бесконечность», — сказал Дэвид Бен-Зви из Техасского университета в Остине.
В последние десятилетия XX века многие математики работали над теорией «категорий бесконечностей» – над тем, что способно отслеживать бесконечную башню эквивалентностей между эквивалентностями. Некоторые из них достигли серьёзного успеха. Но лишь один дошёл до конца.
Переписывая математику
Первая работа Джейкоба Лурье по категориям бесконечности вышла не очень удачной. 5 июня 2003 года 25-летний учёный опубликовал 60-страничный документ под названием «О топосах бесконечности» на сайте научных препринтов arxiv.org. Там он начал делать черновые наброски правил, по которым математики могли бы работать с категориями бесконечности.
Первую работу не все восприняли одинаково. Вскоре после прочтения Питер Мэй, математик из Чикагского университета, написал научному руководителю Лурье, Майклу Хопкинсу, что хотя в работе Лурье и содержатся интересные идеи, она выглядит недоделанной и требует более дисциплинированного подхода.
«Я объяснил наши замечания Майку, а он передал их Джейкобу», — сказал Мэй.
Остаётся неизвестным, воспринял ли Лурье письмо Мэя как вызов, или он уже запланировал свой следующий шаг (Лурье отклонил многочисленные просьбы об интервью). Ясно, что после получения критических замечаний Лурье ударился в многолетний период продуктивности, ставший впоследствии легендарным.
«Я не могу влезть в мозг Джейкоба, и поэтому не знаю точно, о чём он тогда думал, — сказал Мэй. – Но между черновиком, на который мы делали отзыв, и окончательными версиями, которые находятся уже совершенно на другом математическом уровне, существует огромная разница».
В 2006 году Лурье выложил на arxiv.org черновик «Теории высшего топоса». В этой монументальной работе он создал аппарат, необходимый для замены теории множеств новой базой для математики, основанной на категориях бесконечности. «Он создал буквально тысячи страниц этого основополагающего аппарата, который теперь используем все мы», — сказал Чарльз Резк, математик из Иллинойского университета в Урбана-Шэмпейн, проводивший важную работу на раннем этапе разработки категорий бесконечности. «Не могу представить, как можно создать такую работу, как ’Теория высшего топоса’, за всю жизнь – а он создал её за два-три года».
Затем в 2011 году Лурье выдал очередную, ещё более длинную работу. В ней он переизобрёл алгебру.
Алгебра даёт нам прекрасный набор формальных правил манипулирования уравнениями. Математики постоянно используют эти правила для доказательства теорем. Однако алгебра занимается гимнастикой на неподвижных брусьях знака равенства. Уберите эти брусья, заменив их более эфемерной концепцией эквивалентности, и некоторые операции резко усложнятся.
Возьмём одно из первых правил алгебры, которому дети учатся в школе: ассоциативность. Сумма или произведение трёх или более чисел не зависят от их группировки: 2 × (3 × 4) = (2 × 3) × 4.
Легко доказать свойство ассоциативности для списка из трёх и более чисел, если вы работаете с равенством. Это сложно, когда вы работаете даже с понятием сильной эквивалентности. Но когда вы переходите на более тонкие варианты эквивалентности, с их бесконечными башнями путей, соединяющих пути, даже простое правило, подобное ассоциативности, превращается в тёмный лес.
В алгебре ассоциативность утверждает, что (a × b) × c = a × (b × c). Но с применением эквивалентности ассоциативность сама по себе уже не гарантирует, что любая группировка элементов даст один и тот же результат умножения. Этот ассоциаэдр содержит записи эквивалентностей группировок. Каждая вершина соответствует группировке. Рёбра и грани объединяют группировки, ассоциативно эквивалентные друг другу
«Это чрезвычайно усложняет проблему, из-за чего кажется, что с этой новой версией математики работать невозможно», — сказал Дэвид Айла, математик из Университета штата Монтана.
В «Высшей алгебре», последняя версия которой простирается на 1553 страницы, Лурье разработал вариант ассоциативности для категорий бесконечности – а также множество других алгебраических теорем, которые все вместе образуют основу математики эквивалентностей.
Эти две книжки произвели эффект разорвавшейся бомбы; такие работы порождают научную революцию. «Масштаб был чрезвычайным, — сказала Рил. – Это было достижения уровня Гротендика в алгебраической геометрии».
Однако на революции нужно время, и, как обнаружили математики после выхода книг Лурье, эти годы могут быть хаотичными.
Переварить корову
Математики считаются людьми с однозначным мышлением: доказательство либо верное, либо нет; идея либо работает, либо нет. Однако математики являются ещё и обычными людьми, и они реагируют на новые идеи точно так же, как обычные люди: субъективно, эмоционально, имея личные мотивы.
«Думаю, что о математиках написано много текстов в таком тоне, что они ищут сверкающую кристально чистую правду, — сказал Кэмпбел. – Но всё происходит не так. Это люди с собственными вкусами, зонами комфорта, и они могут отрицать не нравящиеся им вещи по эстетическим или личным причинам».
В этом отношении работа Лурье стала сложным вызовом сообществу. По сути, она была провокационной: вот новый и лучший способ заниматься математикой. Это послание было адресовано особенно математикам, всю свою карьеру разрабатывавшим методы, которые превзошёл Лурье.
«Людям не всегда нравится видеть, как следующее поколение переписывает их работу, и этот процесс порождает напряжение, — сказал Фрэнсис. – Это одна из особенностей теории категорий бесконечности – большая часть предыдущих работ переписывается».
Работу Лурье было трудно переварить и по другим причинам. Объёмы материалов означали, что математикам придётся потратить годы на чтение его книг. Это практически невозможно требовать от занятых математиков, находящихся в середине карьеры, а для аспирантов, у которых есть всего несколько лет для того, чтобы выдать результат, позволяющий найти себе работу, это очень рискованно.
Также работа Лурье была очень абстрактной, даже по сравнению с чрезвычайно абстрактной природой всего, что изучает передовая математика. Да и по вкусу она пришлась не всем. «Многие люди считали работу Лурье абстрактной белибердой, а многие просто влюбились в неё, — сказал Кэмпбелл. – Были и промежуточные варианты, включая и тех, кто её вообще не понял».
Эмили Рил
Научное сообщество постоянно воспринимает новые идеи, но обычно это происходит медленно и с ощущением того, что все движутся одновременно. Появление новых идей порождает трудности для интеллектуального аппарата сообщества. «Очень много всего нового появляется сразу – это похоже на то, как удав пытается переварить корову, — сказал Кэмпбелл. – Через сообщество проходит огромная масса».
Если вы – математик, посчитавший, что подход Лурье является лучшим способом заниматься математикой, то ваш путь вперёд будет одиноким. Мало кто читал работы Лурье, не было никаких учебников, пересказывающих их вкратце, и никаких семинаров, помогающих вам сориентироваться. «Способ изучить всё это очень подробно было только один – сесть и самостоятельно всё сделать, — сказал Питер Гейне, аспирант MIT, потративший год на чтение работы Лурье. – Думаю, это самое сложное. Не просто сесть, и самому во всём разобраться – а именно сесть и самому прочитать 800 страниц Теории высшего топоса».
Как и многим новым изобретениям, Теория высшего топоса требует от математиков активного взаимодействия с аппаратом, который позволяет ей работать. Это как заставлять каждого 16-летнего пацана, мечтающего о водительском удостоверении, сначала научиться перебирать двигатель. «Если бы существовала более дружелюбная версия всего этого, то теория сразу же стала бы доступнее для более широких математических кругов», — сказал Деннис Гейтсгори, математик из Гарварда, работавший совместно с Лурье.
Когда люди начали читать работу Лурье и использовать категории бесконечности в своих исследованиях, появились и другие проблемы. Математики строили свои работы на базе категорий бесконечности. Рецензенты из журналов получали эти работы и спрашивали: что это такое?
«Появилась ситуация, в которой работы либо возвращались из журналов обратно с абсурдными рецензиями, из которых было видно полное отсутствие понимания, или на их публикацию уходило по нескольку лет, — сказал Барвик. – Это может доставить много неудобств, поскольку неопубликованная работа, которая лежит у вас на сайте годами, выглядит всё более нелепо».
Однако самой большой проблемой были не неопубликованные работы, а работы, использовавшие категории бесконечности, и опубликованные – но содержавшие ошибки.
Книги Лурье являются единственным авторитетным источником сведений по категориям бесконечности. Они строгие, но их тяжело осознать полностью. И они особенно плохо подходят на роль инструкций, на которые можно было бы ссылаться – сложно искать определённые теоремы, или проверить, что определённое применение категорий бесконечности, встречающееся в чьей-то работе, реально работает.
«Большинство работающих в этой области математиков не читали Лурье систематически, — сказал Андре Жояль, математик из Квебекского университета в Монреале, чья ранняя работа была ключевым ингредиентом книг Лурье. – На это требуется много времени и энергии, поэтому мы просто предполагаем, что всё, что написано в его книгах, верно – потому, что почти каждый раз, когда мы что-нибудь проверяем, оно оказывается верным. На самом деле, каждый раз».
Недоступность книг Лурье привело к появлению неточностей в некоторых из последовавших за ними исследованиях. Книги Лурье сложно читать, сложно цитировать, и сложно использовать для проверки чужих работ.
«Общая литература по теме категорий бесконечности кажется неряшливой», — сказала Захаревич.
Несмотря на весь свой формализм, математика не должна быть сакральным текстом, читать который могут только священники. В этой области требуются не только толстые тома, но и буклеты, не только изначальные откровения, но и интерпретирующие их описания. А пока что теория категорий бесконечностей существует, по большей части, в виде нескольких крупных книг на полке.
«Можно принять подход ’Джейкоб расскажет, что делать, и всё в порядке’, — сказал Резк. – Или можно решить, что ’Мы не знаем, как достаточно хорошо представить нашу тему, чтобы люди смогли ей пользоваться’».
Однако немногие математики смогли принять вызов и сделать категории бесконечностей технологией, которой могли бы пользоваться больше людей из их области исследований.
Дружественная для пользователей теория
Чтобы перевести категории бесконечностей в объект, способный на реальную математическую работу, Лурье пришлось доказывать связанные с ними теоремы. А для этого ему пришлось выбрать ландшафт, на котором можно было бы создавать эти доказательства – так же, как человеку, занимающемуся геометрией, необходимо выбрать для работы систему координат. Математики называют это выбором модели.
Лурье разработал категории бесконечностей на модели квазикатегорий. Другие математики до него разрабатывали категории бесконечностей на других моделях. И хотя их работы были не настолько всеобъемлющими, как у Лурье, в некоторых ситуациях с ними проще иметь дело. «Джейкоб выбрал модель и проверил, что в ней всё работает, но часто она оказывается не самой лёгкой», — сказала Захаревич.
В геометрии математики чётко понимают, как переходить между разными координатными системами. Также они доказали, что теоремы, доказанные в одних условиях, работают и в других.
Для категорий бесконечностей таких гарантий не существует. Однако когда математики пишут работы с использованием категорий бесконечностей, они часто легко переходят между моделями, предполагая (но не доказывая) переносимость результатов. «Люди не уточняют, что делают, переключаются между всеми этими различными моделями, и говорят: А, это одно и то же, — сказал Гейне. – Но это не доказательство».
За последние шесть лет пара математиков пыталась получить эти гарантии. Рил и Доминик Верити из Университета Макуэйра в Австралии, разрабатывали способ описать категории бесконечностей, преодолевающий трудности, появившиеся в предыдущих платформах, использующих те или иные модели. Их работа, основанная на предыдущих трудах Барвика и других, доказала, что многие из теорем «Теории высшего топоса» остаются верными вне зависимости от используемой модели. И доказывают они эту совместимость подходящим образом: «Мы изучаем категории бесконечности, объектами которых служат сами же категории бесконечностей, — сказала Рил. – Теория категорий кусает себя за хвост».
Рил и Верити надеются развивать теорию категорий бесконечностей и ещё одним способом. Они выбирают аспекты теории, работающие вне зависимости от модели. У такой презентации, не зависящей от модели, есть удобное качество мгновенной применимости, которая, как они надеются, привлечёт в эту область исследований математиков, державшихся от неё подальше, когда единственным входом была «Теория высшего топоса».
«Чтобы попасть в этот мир, нужно преодолеть ров, — сказал Хопкинс. – И они занимаются тем, что опускают мост».
Рил и Верити планируют закончить работу в следующем году. Тем временем Лурье недавно начал работу над проектом Kerodon, который он запланировал превратить в нечто вроде справочника по теории высшей категории, похожего на Википедию. Через тринадцать лет после того, как «Теория высшего топоса» формализовала математику эквивалентностей, эти инициативы пытаются уточнить и распространить эти идеи – чтобы сделать математику эквивалентностей более доступной.
«У гениальности важная роль в разработке математики, но само знание является результатом работы всего сообщества, — сказал Жояль. – Реальная цель знания – стать знанием всего сообщества, а не принадлежать одному-двум людям».
Сколько существует видов бесконечности?
Типы бесконечных чисел и некоторые вещи, к которым они относятся:
кардиналов (теория множеств, применяется к размерам ординалов, размерам гильбертовых пространств)
ординалов (теория множеств, используемых для создания порядковых пространств и в порядковом анализе. Некоммутативные.)
чисел Бет (например, кардиналов или нет, в зависимости от континуума гипотезы
гиперреалов (включает в себя бесконечно малые, хороши для анализа, вычислительной геометрии)
суперреалов (максимальные гиперреалы, аналогичные сюрреалам)
сверхъестественных (основные факторы факторизации, используемые в теории поля)
сюрреалов (самая лучшая и самая красивая вещь в мире, максимальное число система, теория комбинаторных игр)
Surcomplex (сюрреалистическая версия комплексных чисел)
Бесконечность исчисления (сводит вещи к пределам)
Бесконечность проективной геометрии (1/0 = бесконечность, положительная бесконечность равна отрицательной бесконечности)
Бесконечное гильбертово пространство любое кардинальное число измерений)
Реальная линия (бесконечная линия, состоящая из всех действительных чисел)
Длинная линия (длиннее, чем действительная линия, в топологии)
Абсолют i nfinity (противоречивый, не очень вещь)
Неограниченные виды чисел:
P-adic (альтернатива действительным числам)
Натуральные числа (1, 2, 3…)
Целые числа (… -3, -2, -1, 0, 1, 2…)
Рациональные числа (1, 1/2, 2/1, 2/3, 3 / 2, 3/4, 4/3…)
Алгебраический (квадрат 2, золотое сечение, все, что вы можете получить с помощью алгебры)
Трансцендентальный (действительные числа, которые вы не можете получить, используя любое конечное количество алгебры, например, пи и е)
Реал (все возможные бесконечные последовательности цифр 0.2 = + 1, но я не 1)
Сплит-кватернионов
Сплит-октонионов
Бикомплексный номер или Гиперкомплекс тессарин
(категория, которая описывает / включает в себя все сложные системы счисления, которые расширяют действительные числа)
Также см. Комбинаторную теорию игр, которая расширяет сюрреалистические числа, чтобы получить числовые, но не совсем числовые значения, такие как «звезда». Звезда путается с нулем, в математическом определении путаницы, но на самом деле это не ноль.
Вы также можете писать действительные числа в других базах, включая отрицательные, иррациональные и даже сложные основания.
,
НЬЮ-ЙОРК. Несмотря на то, что концепция бесконечности существует уже более 2000 лет, она остается загадочной и зачастую сложной идеей для математиков, физиков и философов. Действительно ли существует бесконечность, или это просто часть ткани нашего воображения?
Группа ученых и математиков собралась, чтобы обсудить некоторые глубокие вопросы и противоречия, связанные с концепцией бесконечности, здесь, в пятницу (31 мая), в рамках Всемирного фестиваля науки, ежегодного празднования и исследования науки.
Часть трудностей в попытках решить некоторые абстрактные вопросы, связанные с бесконечностью, заключается в том, что эти проблемы выходят за рамки более устоявшихся математических теорий, говорит Уильям Хью Вудин, математик из Калифорнийского университета в Беркли. [Смотреть: Основные события Всемирного научного фестиваля]
«Математика живет на стабильном острове — мы создали им прочную основу», — сказал Вудин. «Тогда есть дикая земля там. Это бесконечность».
С чего все началось
Философ по имени Элеа Зено, живший с 490 г. до н.э.C. до 430 г. до н.э., приписывают введение идеи бесконечности.
Эту концепцию изучали древние философы, в том числе Аристотель, которые задавались вопросом, могут ли бесконечные существовать в кажущемся конечном физическом мире, сказал Филип Клэйтон, декан Школы богословия Клермонт в Университете Клермонт Линкольн в Клермонте, Калифорния. Теологи, включая Томаса Аквинский использовал бесконечное, чтобы объяснить отношения между людьми, Богом и миром природы.
В 1870-х годах немецкий математик по имени Георг Кантор стал пионером в области, получившей название теории множеств.Согласно теории множеств, целые числа, которые являются числами без дробной или десятичной составляющей (например, 1, 5, -4), составляют бесконечное множество, которое исчисляется. С другой стороны, действительные числа, которые включают целые числа, дроби и так называемые иррациональные числа, такие как квадратный корень из 2, являются частью бесконечного множества, которое неисчислимо.
Это заставило Кантора задуматься о разных видах бесконечности.
«Если теперь есть два вида бесконечности — счетный и непрерывный, более масштабный — есть ли другие бесконечности? Есть ли между ними какая-то бесконечность?» сказал Стивен Строгац, математик из Корнелльского университета в Итаке, штат Северная КаролинаY.
Кантор полагал, что между множествами целых и действительных чисел не существует бесконечности, но он так и не смог доказать это. Его утверждение, однако, стало известно как гипотеза континуума, и математики, которые взялись за проблему по стопам Кантора, были названы теоретиками множеств.
Изучение за пределами
Вудин — теоретик множеств, и всю свою жизнь он пытался разгадать гипотезу континуума. На сегодняшний день математики не смогли доказать или опровергнуть постулату Кантора.Отчасти проблема в том, что идея о том, что существует более двух типов бесконечности, настолько абстрактна, сказал Вудин.
«Нет спутника, который вы могли бы построить, чтобы выйти и измерить гипотезу континуума», — пояснил он. «В нашем мире нет ничего, что помогло бы нам определить, является ли гипотеза континуума истинной или ложной, насколько нам известно». [5 Серьезно умопомрачительных математических фактов]
Более хитрым остается тот факт, что некоторые математики отвергают актуальность этого типа математической работы.
«Эти люди в теории множеств кажутся нам, даже в математике, как-то странными», — пошутил Строгац. Но он сказал, что понимает важность работы, проводимой теоретиками множеств, потому что, если гипотеза континуума окажется ложной, она может вырвать базовые математические принципы так же, как противоречащая теория чисел уничтожит основы математики и физики.
«Мы знаем, что они выполняют действительно глубокую, важную работу, и в принципе это основополагающая работа», — пояснил Строгац.«Они расшатывают основы, над которыми мы все работаем, на втором и третьем этажах. Если они что-то испортят, это может нас всех перевернуть».
Будущее математики
Тем не менее, несмотря на все неопределенности, работа, проведенная теоретиками множеств, может иметь положительный волновой эффект, который служит укреплению основ математики, сказал Вудин.
«Исследуя бесконечность и в той степени, в которой мы можем быть успешными, я думаю, что мы обосновываем последовательность арифметики», объяснил он.«Это немного фанатичное утверждение, но если бесконечность не приводит к противоречию, конечно, конечное не приводит к противоречию. Поэтому, возможно, исследуя внешние границы, чтобы увидеть, есть ли противоречие, вы получаете некоторое безопасность.»
Парадоксы, которые характеризуют концепцию бесконечности, возможно, лучше всего объяснить числом пи, сказал Строгац. Pi, одна из самых узнаваемых математических констант, представляет отношение длины окружности к ее диаметру. Среди множества приложений пи можно использовать для поиска области круга.
«Пи типичен для действительных чисел… в нем содержится бесконечное количество непредсказуемой информации, и в то же время он настолько предсказуем», — сказал Строгац. «Нет ничего более упорядоченного, чем круг, который воплощает пи — это сам символ порядка и совершенства. Так что это сосуществование совершенной предсказуемости и порядка с этой мучительной тайной бесконечной загадки, встроенной в один и тот же объект, является частью удовольствия наш предмет и, я полагаю, сама бесконечность.»
Следите за Дениз Чоу в Твиттере @denisechow . Следуйте LiveScience @livescience , Facebook & Google+ . Оригинальная статья на LiveScience.com.
,
БЕСКОНЕЧНОСТЬ | определение в кембриджском словаре английского языка
Тезаурус: синонимы и родственные слова
,
Знаете ли вы, верно ли это неравенство?
![clip_image002[3]](/800/600/http/igoro.com/wordpress/wp-content/uploads/2011/04/clip_image00232.gif "clip_image002[3]")
Это простой вопрос, но с интригующим и откровенным ответом.
Infinity # 1
Одна из концепций бесконечности, с которой большинство людей встречалось бы на уроках математики, — это бесконечность пределов. С ограничениями мы можем попытаться понять 2 ∞ следующим образом:
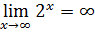
Символ бесконечности используется здесь дважды: первый раз для представления «по мере роста x», а второй раз для представления «2 x в конечном итоге навсегда превысит любую конкретную границу».
Если мы используем обозначение немного свободно, мы могли бы «упростить» вышеуказанный предел следующим образом:
![clip_image002[4]](/800/600/http/igoro.com/wordpress/wp-content/uploads/2010/05/clip_image0024.gif "clip_image002[4]")
Это предполагает, что ответом на вопрос в названии является «Нет», но, как вскоре станет ясно, использование произвольной записи бесконечности не является хорошей идеей.
Infinity # 2
Помимо пределов, в математике есть еще одно место, где важна бесконечность: в теории множеств.
Теория множеств распознает бесконечности нескольких «размеров», наименьшим из которых является набор натуральных чисел: {1, 2, 3,…}.Набор, размер которого равен размеру положительного целого набора, называется , счетно бесконечным, .
- «Счетная бесконечность плюс один»
Если мы добавим еще один элемент (скажем, 0) к набору натуральных чисел, будет ли новый набор больше? Чтобы увидеть, что он не может быть больше, вы можете посмотреть на проблему по-другому: в наборе {0, 1, 2,…} каждый элемент просто на единицу меньше по сравнению с множеством {1, 2, 3,…}. Таким образом, хотя мы добавили элемент к бесконечному набору, мы на самом деле просто « перемаркировали » элементов, уменьшая каждое значение.
- «бесконечность, умноженная вдвое»
Теперь давайте «удвоим» набор натуральных чисел, добавив значения 0,5, 1,5, 2,5,… Новый набор может показаться больше, поскольку он содержит бесконечное число новых значений. Но опять же, вы можете сказать, что наборы имеют одинаковый размер, просто каждый элемент в два раза меньше: - «Счетная бесконечность в квадрате»
Чтобы «вычислить» счетную бесконечность, мы можем сформировать набор, который будет содержать все целые пары , такие как [1,1], [1,2], [2,2] и скоро.Соединяя каждое целое число с каждым целым, мы эффективно возводим в квадрат размер набора целых чисел.Могут ли пары целых чисел быть в основном просто помечены целыми числами? Да, они могут, и поэтому набор целочисленных пар не больше, чем набор целых чисел. На диаграмме ниже показано, как целочисленные пары могут быть «помечены» обычными целыми числами (например, пара [2,2] помечена как 5):
- «Два к степени счетной бесконечности»
Набор целых чисел содержит счетную бесконечность элементов, и поэтому набор всех целых подмножеств должен — грубо говоря — содержать два в степени счетной бесконечности элементов ,Итак, равняется ли число целых подмножеств количеству целых? Оказывается, что уловка «перемаркировки», которую мы использовали в первых трех примерах, здесь не работает, и, таким образом, оказывается, что на больше целых подмножеств , чем целых чисел.
Давайте посмотрим на четвертый пример более подробно, чтобы понять, почему он так принципиально отличается от первых трех. Можно представить целое подмножество как двоичное число с бесконечной последовательностью цифр: i -ая цифра равна 1, если i включено в подмножество, и 0, если i исключено.Таким образом, типичное целочисленное подмножество — это последовательность единиц и нулей, идущая вечно, без появления паттернов.
И теперь мы подходим к ключевой разнице. Каждая пара целых, полуцелых или целых чисел может быть описана с использованием конечного числа битов . Вот почему мы можем щуриться от набора целочисленных пар и видеть, что на самом деле это просто набор целых чисел. Каждая целочисленная пара может быть легко преобразована в целое число и обратно.
Однако целое подмножество представляет собой бесконечной последовательности битов.Невозможно описать общую схему преобразования бесконечной последовательности битов в конечную последовательность без потери информации. Вот почему невозможно прищуриться на множестве целочисленных подмножеств и утверждать, что это действительно набор целых чисел.
На схеме ниже показаны примеры бесконечных множеств трех разных размеров:
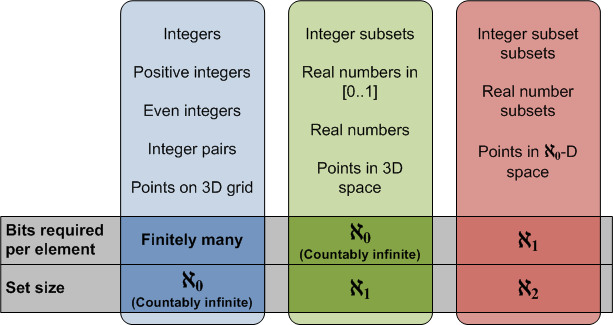
Итак, в теории множеств существует множество бесконечностей. Наименьшая бесконечность — это «исчисляемая» бесконечность,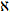 
0 , которая соответствует числу целых чисел.Большая бесконечность — 
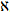1 , что соответствует количеству действительных чисел или целых подмножеств. И есть еще больше и больше бесконечных множеств.
Поскольку целых подмножеств больше, чем целых, неудивительно, что приведенная ниже математическая формула справедлива (формулу можно найти в статье Википедии о гипотезе континуума):
![clip_image002[4]](/800/600/http/igoro.com/wordpress/wp-content/uploads/2011/04/clip_image0024.png "clip_image002[4]")
И так как 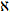0 обозначает бесконечность (наименьший вид), кажется, что это не будет большой натяжкой, чтобы написать это:
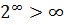
… и теперь кажется, что ответ на вопрос из заголовка должен быть «Да».
Ответ
Итак, правда ли, что 2 ∞ > ∞? Ответ зависит от того, какое понятие бесконечности мы используем. Бесконечность пределов не имеет понятия о размере, и формула будет ложной. У бесконечности теории множеств действительно есть понятие размера, и формула была бы отчасти верна.
Технически утверждение 2 ∞ > ∞ не является ни истинным, ни ложным. Из-за неоднозначных обозначений невозможно сказать, какая концепция бесконечности используется и, следовательно, какие правила применяются.
Кого это волнует?
Хорошо … но почему кого-то волнует, что существуют два разных понятия бесконечности? Легко создать впечатление, что обсуждение — это просто интеллектуальное упражнение без практических последствий.
Напротив, строгое понимание двух видов бесконечности было очень важно. После правильного понимания первого вида бесконечности Исаак Ньютон смог разработать исчисление, после чего последовала теория гравитации. И второй вид бесконечности был предварительным условием для Алана Тьюринга для определения вычислимости (см. Мою статью о числах, которые не могут быть вычислены) и для Курта Геделя для доказательства теоремы Гёделя о неполноте.
Итак, понимание обоих видов бесконечности привело к важным идеям и практическим достижениям.
,