Треугольники ру: Треугольники

Треугольники

Признак принадлежности четырёх точек одной окружности

 Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

∠ABD=∠ACD

Доказать: точки A, B, C, D лежат на одной окружности

Доказательство:

Читать далее

Окружность

Теорема (свойство вписанного четырёхугольника)

Сумма противолежащих углов вписанного четырёхугольника равна 180°.

Дано: ABCD вписан в окр. (O; R)

Доказать:

∠A+∠C=180°,

∠B+∠D=180°.

Доказательство:

Читать далее

Окружность

Рассмотрим задачи в которых известна сумма углов параллелограмма.

Сумма всех четырёх углов параллелограмма равна 360° (как сумма углов выпуклого четырёхугольника).

Для параллелограмма ABCD

∠A+∠B+∠C+∠D=360°.

Читать далее

Параллелограмм

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

Дано: ABCD — трапеция, AD||BC,

F — середина AC, K — середина BD,

MN — средняя линия трапеции

Доказать: FK∈MN,

Читать далее

Трапеция

Замечательное свойство трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

ABCD- трапеция, AD||BC,

AB∩CD=F, AC∩BD=O,

FO∩AD=K, FO∩BC=P

Доказать:  K- середина AD,

P- середина BC

Доказательство:

Читать далее

Трапеция

Утверждение 1

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, делится этой точкой пополам.

Дано: ABCD — трапеция, AD||BC,

AC∩BD=O, F∈AB, K∈CD,

FK||AD, O∈FK

Доказать: O — середина FK.

Доказательство:

Читать далее

Трапеция

Утверждение

Медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.

Дано: ΔABC,

BM — медиана,

D∈AB, E∈BC, DE||AC,

DE∩BM=F

Доказать: DF=FE

Доказательство:

Читать далее

Элементы треугольника

1
2
3
4
…
70
Далее →

Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Рассмотрим важные теоремы, которые помогут нам при решении задач.

Теорема 1. Вокруг любого треугольника можно описать окружность, причем только одну. Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.

Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.

Доказательство этой теоремы здесь: Свойство серединных перпендикуляров.

Теорема 2. В любой треугольник можно вписать окружность, причем только одну. Ее центром является точка пересечения биссектрис треугольника.

Доказательство теоремы здесь: Свойства биссектрис треугольника.

Теорема 3. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.

Доказательство:

Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Его доказательство можно найти здесь: Свойство медианы прямоугольного треугольника.

Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.

Теорема 4.

Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.

Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.

Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.

Теорема 5. Радиус окружности , вписанной в прямоугольный треугольник с катетами и и гипотенузой , вычисляется по формуле:

Доказательство теоремы здесь: Радиус окружности, вписанной в прямоугольный треугольник.

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Напомним определение правильного многоугольника:

Правильным называется многоугольник, все стороны и все углы которого равны. Центры вписанной и описанной окружностей правильного многоугольника находятся в одной точке.

Из этого определения, понятно, что правильный треугольник – равносторонний. Для решения такого треугольника полезно уметь выводить формулы радиусов вписанной и описанной окружностей.

Теорема 6.

Для правильного треугольника со стороной а радиус описанной окружности равен

А радиус окружности, вписанной в правильный треугольник, равен

Докажем эту теорему.

У равностороннего треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.

Пусть в правильном треугольнике стороны , точка О – центр вписанной и описанной окружностей, — медианы и высоты. По свойству медиан треугольника, отрезки в точке О делятся в отношении 2 : 1, считая от вершин. Тогда

Получаем, что

Из треугольника АВН получаем, что длина стороны

Тогда

Значит, формула радиуса окружности, описанной около правильного треугольника —

Формула радиуса окружности, вписанной в правильный треугольник

Как видим, часто геометрическая задача решается с помощью несложных формул, и помогает в этом алгебра.

Разберем задачи ОГЭ и ЕГЭ по теме: Вписанные и описанные треугольники.

Задача 1, тренировочная. Периметр правильного треугольника АВС равен 15. Найдите радиус вписанной и описанной окружностей.

Решение:

Длина стороны равностороннего треугольника  равна

Радиусы – вписанной и – описанной окружностей можно найти по формулам:

где — сторона треугольника.

Значит,

Ответ:

Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.

Вот две полезные формулы для площади треугольника.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

,

где — полупериметр,

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Теорема синусов:

R — радиус описанной окружности

Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.

Решение:

Выразим площадь треугольника двумя разными способами:

где – полупериметр треугольника, a – его стороны.

Тогда , а диаметр окружности равен

Ответ: 8.

Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Решение:

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что .

Тогда .

В ответ запишем .

Ответ: 4.

Задача 4, ЕГЭ. В треугольнике сторона равна  , а угол равен . Найдите радиус описанной около этого треугольника окружности.

Решение:

По теореме синусов

Тогда

Ответ: 7.

Задача 5, ЕГЭ. В треугольнике угол А равен , а угол В – . Найдите радиус окружности, описанной около треугольника , если сторона равна 10.

Решение:

Зная, что сумма углов треугольника равна , найдем угол С.

По теореме синусов

Значит,

Ответ: 10.

Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

Ответ: 150.

Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем .

Тогда .

Ответ: 25.

Задача 8, ОГЭ. В равнобедренном треугольнике основание равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.

Решение:

Высота , проведенная к основанию , является медианой. Значит, .

находится по теореме Пифагора из треугольника :

Периметр треугольника – это сумма длин сторон, т.е.

Площадь треугольника

Радиус вписанной окружности r найдем по формуле

Ответ:

Задача 9, ОГЭ. Стороны и треугольника равны 6 и соответственно, угол . Найдите диаметр окружности, описанной около треугольника .

Решение:

Найдем длину стороны по теореме косинусов, используя длины сторон , и косинус угла В, противолежащего стороне :

Теперь воспользуемся теоремой синусов:

Значит, диаметр окружности, описанной около треугольника , равен 6.

Ответ: 6.

Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.

Решение:

Пусть длина радиуса описанной окружности , а длина радиуса вписанной окружности

Мы знаем, что , где – полупериметр,  – стороны треугольника.

Значит,

Отсюда

Тогда

Ответ: 11.

Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.

Решение:

Пусть радиус вписанной окружности , а гипотенуза

Мы знаем, что в прямоугольном треугольнике

Значит, отсюда

Площадь находится по формуле где – полупериметр,  – стороны треугольника.

Ответ: 24.

Рассмотрим также задачу из 2 части ЕГЭ по математике.

Задача 12. Точка О – центр вписанной в треугольник окружности. Прямая вторично пересекает описанную около треугольника окружность в точке Р.

а) Докажите, что

б) Найдите площадь треугольника , если радиус окружности, описанной около треугольника равен 10,

Решение:

а) Пусть О – центр вписанной окружности, значит, и – биссектрисы углов и соответственно, и

как вписанные углы, опирающиеся на одну и ту же дугу
Тогда

– внешний угол треугольника , поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.

Значит, Что и требовалось доказать.

б)  , следовательно, треугольник – равнобедренный, – основание,

Угол равен , значит,

По теореме синусов для треугольника :

Тогда отрезок равен отрезку , т.е. .

Найдем угол С из треугольника :

как вписанные углы, опирающиеся на дугу .

Площадь треугольника находится по формуле:

Ответ:

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Круговой треугольник Рело / Этюды // Математические этюды

Круговой треугольник Рело / Этюды // Математические этюды

Математические этюды

Вернуться к списку

Вот и «Луч-2», восьмимиллиметровый кинопроектор. Он был в каждом русском доме, где кинолюбители снимали и смотрели фильмы.

В этой карикатуре представлено геометрическое понятие, часто изучаемое в математических кружках, и его применение в нашей повседневной жизни.

Колесо… Круг. Одним из свойств круга является его постоянная ширина. Нарисуем две параллельные линии и зафиксируем расстояние между ними. Давайте начнем их вращать. Кривая (в данном случае круг) постоянно касается обеих линий. Это определение того, что замкнутая кривая имеет постоянную ширину.

Существуют ли кривые, отличные от окружностей постоянной ширины?

Рело, Франц 1829—1905

Французский ученый. Был первым (1875 г.) правильно сформулировал основные вопросы строения и кинематики механизмов; разрабатывал проблемы проектирования технических механизмов.

Рассмотрим правильный треугольник. На каждой стороне треугольника начертим дугу окружности радиусом, равным длине стороны. Эта кривая называется треугольником Рело. Оказывается, это кривая постоянной ширины. Как и в случае с кругом, проведем две касательные, зафиксируем расстояние между ними и начнем их вращать. Наша кривая постоянно касается обеих линий. Действительно, одна из точек касания всегда находится на одном из «углов» треугольника Рело, а другая — на противоположной дуге окружности. Поэтому ширина всегда равна радиусу окружностей, т.е. равна длине стороны исходного треугольника.

В бытовом смысле постоянная ширина кривой означает, что если сделать колеса с таким профилем, то книга будет катиться по ним, не шевелясь.

Однако сделать колесо с таким профилем невозможно, так как центр этой фигуры описывает сложную линию при качении.

Существуют ли другие кривые постоянной ширины? Оказывается, их бесконечно много.

На любом правильном многоугольнике с нечетным числом вершин можно построить кривую постоянной ширины по схеме построенного треугольника Рело. Необходимо провести дугу окружности, соединяющую концы противоположной стороны и центра в каждой вершине. В Англии монета номиналом 20 пенсов имеет форму кривой постоянной ширины, построенной на семиугольнике.

Рассматриваемые кривые не исчерпывают весь класс кривых постоянной ширины. Оказывается, существуют несимметричные кривые постоянной ширины. Мы рассматриваем произвольный набор пересекающихся прямых. Затем рассматриваем один из секторов. Проведем дугу окружности с центром в точке пересечения линий, определяющих этот сектор, и случайным радиусом. Затем рассмотрим следующий сектор и проведем окружность с центром в точке пересечения линий, ограничивающих этот сектор. Радиус выбирается так, чтобы часть уже нарисованной кривой можно было непрерывно удлинять. Продолжим наше построение дальше. Получается, что кривая замкнется и мы получим кривую постоянной ширины. Докажи это

Все кривые заданной ширины имеют равные периметры. Окружность и треугольник Рело выделяются из всех остальных кривых заданной ширины своими экстремальными свойствами. Окружность ограничивает наибольшую площадь, а треугольник Рело — наименьшую.

Треугольник Рело часто изучают в математических кружках. Оказывается, у этой геометрической фигуры есть интересные приложения в механике.

Смотри, это Mazda RX-7. В отличие от большинства серийных автомобилей он (а также модель RX-8) оснащен роторным двигателем Ванкеля. Как это устроено? В качестве ротора используется треугольник Рело! Ротор разделяет камеру на три части, каждая из которых по очереди становится камерой сгорания. Сначала впрыскивается топливно-воздушная смесь синего цвета, затем за счет движения ротора она сжимается, воспламеняется и закручивает ротор. Роторный двигатель лишен некоторых недостатков свободнопоршневого двигателя. Например, здесь вращение передается непосредственно на ось и не обязательно использовать коленчатый вал.

А это когтевой механизм. Он использовался в кинопроекторах. Двигатели дают равномерное вращение оси. Но для резкого изображения необходимо тянуть пленку на один кадр, останавливать, а потом снова быстро тянуть. И так 18 раз в секунду. Коготь-механизм решает эту проблему. В его основе треугольник Рело, вписанный в квадрат, и два параллелограмма, препятствующие его отклонениям. Действительно, так как длины противоположных сторон равны, то среднее сечение, основание и сторона квадрата всегда параллельны друг другу. Чем ближе ось зажима к вершине треугольника Рело, тем ближе фигура, описываемая зубочелюстным аппаратом, к квадрату.

Можно было бы подумать, что чисто математические задачи находят интересные приложения.

Другие этюды из раздела «Кривые постоянной ширины»

Сверление квадратных отверстий Изобретение колеса

Математические этюды

Будущее большого треугольника — Россия в глобальной политике раз я не уверен в завтрашнем дне. К множеству уже предсказанных спорных проблем и тенденций добавляется «черный лебедь» — эпидемия коронавируса.

Это серьезная проблема для многих стран, особенно для Италии. Но с исторической точки зрения это относительно распространенная эпидемия. Если это может серьезно повлиять на глобальное развитие, то по двум причинам. Создается впечатление, что правящие элиты многих стран используют его, чтобы скрыть свои прошлые неудачи или оправдать свою неспособность справиться с вызовами, с которыми они сталкиваются. К верхним относятся загрязнение окружающей среды и изменение климата, быстрое обнищание среднего класса, рост социального неравенства и, наконец, исчерпание нынешней модели капитализма, призванной стимулировать постоянно растущее потребление. Попытки прикрыть и оправдать подняли вопрос о коронавирусе на площадь, а современные СМИ возвели его в третью степень.

Итак, эпидемия действительно может иметь поистине исторические последствия, но какими именно они будут, никто не знает.

И все же я принял просьбу главного редактора журнала Limes сделать прогноз и оценить развитие отношений в треугольнике великих держав—России, Китая и США—от Русская точка зрения. Я рискну.

Для удобства я пойду по сценарию, который считаю наиболее вероятным. Основные тенденции последних лет — частичная экономическая деглобализация, ренационализация мировой политики и экономики, усиление соперничества между США и Китаем, ослабление ЕС и многосторонних институтов в целом — будут усугубляться происходящим в настоящее время глубоким глобальным экономическим кризисом. Все будет как сегодня, но еще хуже.

Единственным светлым пятном в этом прогнозе является возможное частичное удаление паразитарных бородавок с тела современных обществ и экономик – сдувание финансовых и информационных пузырей, которые все чаще служили заменой реальной экономики и жизни. Семья, вера, самореализация, прежде всего, через служение обществу и стране, скорее всего, вернут себе центральное место. Профессии инженера, врача, полицейского и людей, которые делают что-то реальное, снова станут самыми важными. На самом деле эти ценности никогда не переставали существовать в незападном мире.

*   *   *

Треугольник ведущих держав является виртуальной конструкцией из-за нежелания США сотрудничать с кем бы то ни было в надежде дать последний отпор своей ослабевающей гегемонии. Треугольник распадается на три пары отношений.

Российско-американские отношения никогда не были такими враждебными с 1950-х годов. США раздражал отказ России идти по стопам американского лидерства и сам факт ее возрождения. Кроме того, восстановив свою стратегическую мощь, Россия, по-видимому, лишила США и Запад в целом их военного превосходства — основы их пятисотлетнего доминирования в политике, экономике и культуре, позволившей ей выкачивать от валового мирового продукта в свою пользу. Россия, как и прежде Советский Союз, больше всего пыталась обеспечить собственную безопасность, но попутно и невольно стала причиной этой исторической трансформации.

США встали на путь конфронтации в начале 2010-х годов. Когда в 2014 году Россия остановила экспансию западных альянсов, присоединив к себе Крым и поддержав мятежный Донбасс, конфронтация стала очевидной. Обама надеялся уничтожить Россию и «разорвать ее экономику на куски». Команда Трампа планировала оказать сильное давление на Россию, чтобы оторвать ее от Китая. Но обе стратегии дали противоположные результаты. Хотя санкции замедлили ее экономическое развитие, Россия не сдалась, консолидировалась внутри страны и углубила сотрудничество с Китаем.

Но попутно американская элита продала себе идею — совершенно ложную, как теперь всем очевидно, — что Россия массово вмешивалась в выборы в США и поддерживала Трампа. Эта пропаганда стала важным фактором американской внутриполитической борьбы. В этой ситуации вряд ли можно ожидать скорой нормализации отношений, хотя Москва и пытается исправить положение. Ему не нужен нынешний уровень враждебности.

На самом деле это просто опасно. Вкупе с ухудшением ситуации в военно-технической сфере — в мире появляется все больше дестабилизирующего оружия, сносятся оставшиеся режимы ограничения вооружений, деградирует интеллектуальный уровень и ответственность элит ряда стран — эта враждебность повышает вероятность непреднамеренной войны и ее эскалации до уровня глобальной ядерной катастрофы. Нынешняя политика Москвы в отношении США держится на трех китах: попытках снизить уровень конфронтации; сильное, даже упреждающее, военное сдерживание, включая создание оружия, делающего надежды Запада на восстановление стратегического превосходства непомерно дорогими; активизация экономических, политических и военных отношений с незападным миром, дальнейшее продвижение многополярности. Почти никто в Москве больше не ожидает улучшения отношений с США в ближайшие годы. Учитывая внутренние разногласия в США, она выглядит крайне ненадежным партнером.

Россия продолжает усилия по относительной нормализации отношений с Европой, но и в этом есть много скептицизма. Европейский Союз слишком неэффективен и все больше погружается в проблемы, созданные его собственным медленным распадом. Европейцы по-прежнему сильно зависят от Соединенных Штатов, что во многом им невыгодно. Наконец, стало ясно, что современные западные демократии не могут существовать без врага. В прошлом это был коммунизм и Советский Союз. Когда их не стало, западные элиты праздновали победу, но вскоре увидели, что их общества выходят из-под контроля («популисты»), а привычные отношения (атлантизм) разваливаются. Вот они и стали изобретать врага, выбрав, как обычно, Россию, которая «подрывает демократию», то есть разрушает установленный порядок. Но он рушится сам по себе из-за внутренних противоречий, и Москва здесь ни при чем. Особенно смехотворны обвинения в том, что Россия представляет военную угрозу. И это при том, что Россия значительно сократила свои вооруженные силы и ее расходы на оборону намного меньше, чем у одних только европейских стран НАТО.

Усиление конфронтации со стороны Запада дало мощный толчок повороту России на восток. Он начался во второй половине 2000-х годов в основном как экономический проект, призванный задействовать потенциал растущих азиатских рынков, уйти от чрезмерной зависимости от западных рынков и освоить восточные территории, которые выглядели опасным вакуумом рядом с растущим Китаем.

Но по мере усиления давления Запада «поворот на Восток» начал приобретать геополитические очертания. Хотя разворот все еще не завершен, он привел к качественным изменениям: объем торговли с Азией сравнялся с объемом торговли с Европой, которая когда-то преобладала.

Россия создала новое качество отношений с Китаем , вероятной сверхдержавой номер один в будущем. Они были дружны, теперь они стали полусоюзными, «независимыми» при необходимости, «но никогда друг против друга». Китай стал растущим внешним источником капитала, технологий и рынков сбыта для России и ее продукции, в первую очередь нефти и газа, сырья и растущей сельскохозяйственной продукции. Но самое главное, Россия обеспечила безопасность своих восточных границ и даже помогает Китаю создать систему раннего предупреждения о ракетном нападении, которая укрепляет безопасность обеих стран и расширяет возможности стратегического сдерживания против США. Это позволяет Китаю полагаться на стратегическую мощь России в противодействии давлению США. Россия, в свою очередь, может рассчитывать на экономическую мощь Китая. Когда конфронтация с Западом была на пике, Пекин, насколько известно, предлагал почти неограниченное кредитование, но Москва решила идти своим ходом. Две страны договорились не конкурировать друг с другом в Центральной Азии.

Но элементы соревнования присутствуют. Несмотря на очень тактичную политику Пекина, Россия по-прежнему обеспокоена своей чрезмерной властью, особенно из-за ее все более наступательной, хотя и не агрессивной политики в отношении более мелких и зависимых стран.

Сближение выгодно обеим странам сейчас и будет таковым в ближайшие годы. Поворот России на Восток и ее сближение с Китаем качественно изменили баланс сил в отношениях с Западом в пользу Москвы. Россия превратилась из подмастерья, готового платить за обучение и прием в клуб, каким она была или казалась 10-15 лет назад, в балансир и центральную евразийскую державу; это «возвращение домой» геополитически и идеологически. Будучи в основном европейской в ​​культурном отношении, Россия в значительной степени является азиатской в ​​политическом и социальном отношении. Без сверхцентрализации, сильной авторитарной власти и Сибири с ее несметными богатствами страна не была бы тем, чем она является сегодня и что определяет ее генетический код как великой державы. Несмотря на колоссальные различия в культуре, Россия и Китай имеют много общего в истории. До 15 века оба были завоеванными частями Монгольской империи, самой большой из когда-либо известных миру. Разница лишь в том, что Китай ассимилировал монголов, а Россия их вытеснила, но впитала в себя многие азиатские черты за два с половиной века их правления. В период уходящего пятисотлетнего лидерства Европы и Запада «азиатскость» считалась признаком отсталости. Но сейчас это, похоже, становится конкурентным преимуществом как с точки зрения возможности концентрировать ресурсы для жесткой конкуренции, так и с точки зрения борьбы с новыми вызовами, в частности, с коронавирусом. Технологически Азия тоже ушла далеко вперед.

Соперничество между США и Китаем , вероятно, продолжится или даже усилится. Вопреки рекомендациям своих последних стратегов — Генри Киссинджера и покойного Збигнева Бжезинского — американская элита сделала выбор в пользу почти всесторонней конфронтации с Китаем, по сути, новой холодной войны. Его единственная надежда — использовать позиции, оставшиеся от прежней экономической системы, для «последнего боя». Но, вероятно, уже слишком поздно. Баланс сил в мире резко изменился. Он стал гораздо более гибким, отчасти благодаря тому, что Россия лишила Запад возможности диктовать свою волю и силой навязывать свои интересы. Теперь меньше стран будут готовы следовать политике США.

В случае дальнейшего обострения соперничества США и Китая Россия не будет «бросать» Китай, а будет искать и уже ищет пути расширения пространства для маневра, пытаясь улучшить отношения с некоторыми европейскими странами и сблизиться с ключевыми азиатскими странами, такими как Индия, Япония, Южная Корея, Вьетнам, Турция, Иран, Египет, Саудовская Аравия и страны АСЕАН.

Не думаю, что существует серьезный риск для России оказаться в стратегической зависимости от Китая. Никакая зависимость от какого-либо внешнего центра неприемлема для России с ее священным стремлением к суверенитету. Это не может быть чей-то «младший брат».

Когда Запад попытался превратить его в единое целое, он встретил твердый отпор. Китай знает об этом опыте так же, как осознает тот факт, что Россия выбила или победила всех, кто стремился к мировой или региональной гегемонии — наследников Чингисхана, Карла XII, Наполеона и Гитлера.

Россия самодостаточна в военном и политическом отношении.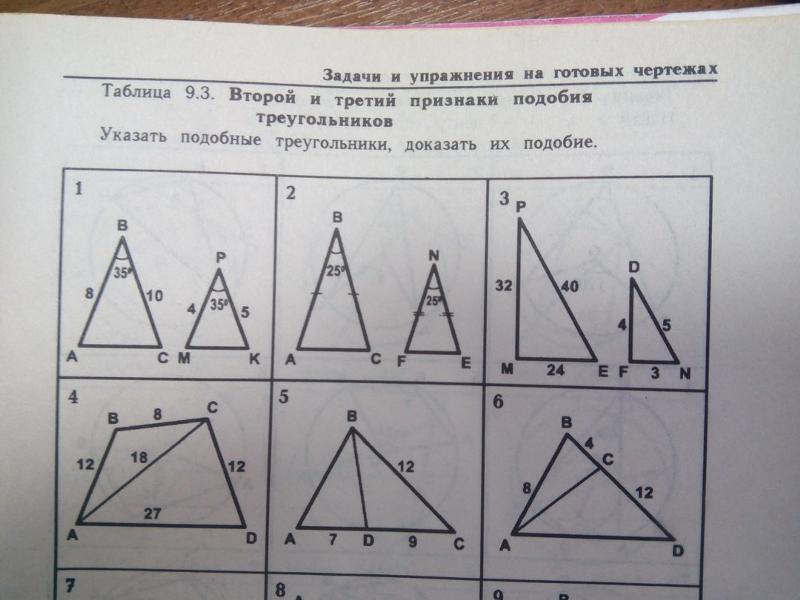 Но ему нужны зарубежные рынки и партнеры для экономического, технологического и цифрового развития. И будет их искать и находить.

К сожалению, третий столп будущего мирового порядка, третья технологическая платформа так и не материализовалась. Он был бы создан, если бы Европа, опьяненная эйфорией и пораженная стратегическим помешательством в XIX90-х, не отказались от идеи построения общего пространства с Россией. Но Россия по-прежнему горит желанием начать новый виток сближения с Европой с учетом нового баланса сил и новых реалий, но уже в рамках евразийской стратегии.

Появятся два мягких суперцентра. Одна Америка плюс: англосаксы и часть европейцев. С колебаниями и мучениями США придется отказаться от роли глобальной сверхдержавы, невыгодной в новом мире, где они уже не могут диктовать свои условия.

Будущее китайского «центра» не очевидно. Если Китай последует тысячелетней традиции Поднебесной и попытается превратить своих партнеров в вассалов, Россия, Индия, Турция, Иран, Япония, Вьетнам и многие другие будут сопротивляться. В этом случае Китай останется просто могущественным государством с сетью зависимых стран в Азии, Африке и Латинской Америке.

Москва предлагает другой вариант: создание Большого Евразийского партнерства, официально поддержанного Пекином, как системы равноправных экономических, политических, культурных, цивилизационных связей и интеграционных объединений, где Китай был бы первым среди равных. Это партнерство в той или иной форме будет охватывать значительную часть западной оконечности Евразии—Европы. Уже очевидно, что при таком сценарии его северная и западная части будут больше тяготеть к американскому центру, а юг и центр — к евразийскому проекту.

Россия сможет быть полезна в обоих случаях либо как балансир между двумя потенциальными гегемонами и гарант нового неприсоединения, либо как один из активных созидателей нового партнерства, разворачивающегося с окраин Европы и Азии в Северную Евразию, один из ее ключевых центров.

__________________________

Эта статья изначально была написана для публикации в журнале Limes.